You can use the right-triangle trick to find the area of a trapezoid. The following trapezoid TRAP looks like an isosceles trapezoid, doesn’t it? Don’t forget — looks can be deceiving.
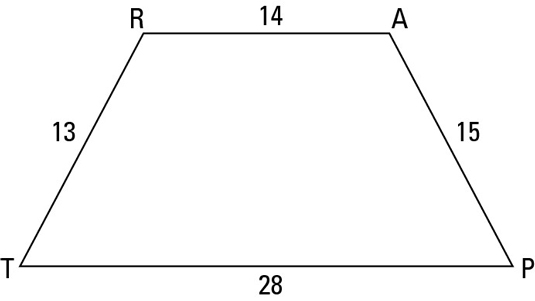
You should be thinking, right triangles, right triangles, right triangles. So draw in two heights straight down from R and A as shown in the following figure.
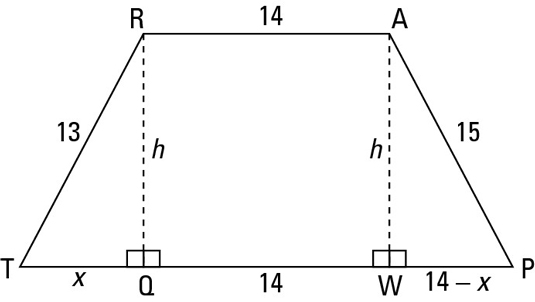
You can see that QW, like RA, is 14. Then, because TP is 28, that leaves 28 – 14, or 14, for the sum of TQ and WP. Next, you can assign segment TQ a length of x, which gives segment WP a length of 14 – x. Now you’re all set to use — what else? — the Pythagorean Theorem. You have two unknowns, x and h, so to solve, you need two equations:
Now solve the system of equations. First, you subtract the second equation from the first, column by column:







