In physics, when an object travels in uniform circular motion, its speed is constant, which means that the magnitude of the object’s velocity doesn’t change. Therefore, acceleration can have no component in the same direction as the velocity; if it did, the velocity’s magnitude would change.
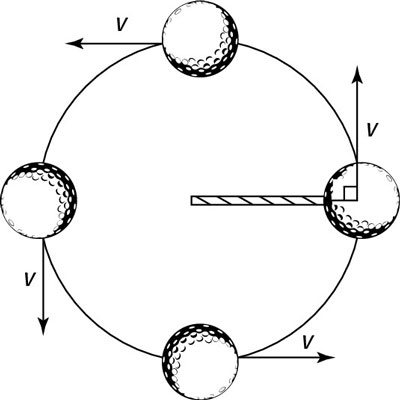
However, as this figure shows, the velocity’s direction is constantly changing — it always bends so that the object maintains movement in a constant circle. To make that happen, the object’s centripetal acceleration is always directed toward the center of the circle, perpendicular to the object’s velocity at any one time. The acceleration changes the direction of the object’s velocity while keeping the magnitude of the velocity constant.
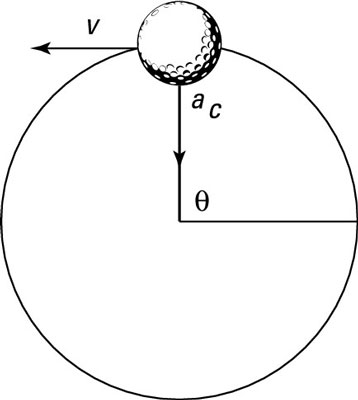
In the example shown here, the string exerts a force on the ball to keep it going in a circle — a force that provides the ball’s centripetal acceleration. In order to provide that force, you have to constantly pull on the ball toward the center of the circle. (Picture what it feels like, force-wise, to whip an object around on a string.) You can see the centripetal acceleration vector, ac, in the figure.
If you accelerate the ball toward the center of the circle to provide the centripetal acceleration, why doesn’t it hit your hand? The answer is that the ball is already moving at a high speed. The force, and therefore the acceleration, that you provide always acts at right angles to the velocity.
You always have to accelerate an object toward the center of the circle to keep it moving in circular motion. So can you find the magnitude of the acceleration you create? No doubt. If an object is moving in uniform circular motion at speed v and radius r, you can find the magnitude of the centripetal acceleration with the following equation:
For a practical example, imagine you’re driving around curves at a high speed. For any constant speed, you can see from the equation that the centripetal acceleration is inversely proportional to the radius of the curve. In other words, on tighter curves (as the radius decreases), there needs to be a greater centripetal acceleration (provided by the friction between the tires and the road).

