Analyze a First-Order RL Circuit Using Laplace Methods

Using the Laplace transform as part of your circuit analysis provides you with a prediction of circuit response. Analyze the poles of the Laplace transform to get a general idea of output behavior. Real poles, for instance, indicate exponential output behavior.

Follow these basic steps to analyze a circuit using Laplace techniques:

1. Develop the differential equation in the time-domain using Kirchhoff’s laws and element equations.

2. Apply the Laplace transformation of the differential equation to put the equation in the s-domain.

3. Algebraically solve for the solution, or response transform.

4. Apply the inverse Laplace transformation to produce the solution to the original differential equation described in the time-domain.

To get comfortable with this process, you simply need to practice applying it to different types of circuits such as an RC (resistor-capacitor) circuit, an RL (resistor-inductor) circuit, and an RLC (resistor-inductor-capacitor) circuit.

Here is an RL circuit that has a switch that’s been in Position A for a long time. The switch moves to Position B at time t = 0.

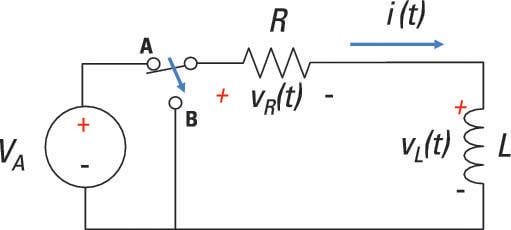
For this circuit, you have the following KVL equation:

v_R(t) + v_L(t) = 0

Next, formulate the element equation (or i-v characteristic) for each device. Using Ohm’s law to describe the voltage across the resistor, you have the following relationship:

v_R(t) = i_L(t)R

The inductor’s element equation is

Substituting the element equations, v_R(t) and v_L(t), into the KVL equation gives you the desired first-order differential equation:

On to Step 2: Apply the Laplace transform to the differential equation:

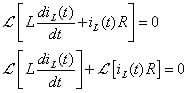
The preceding equation uses the linearity property which says you can take the Laplace transform of each term. For the first term on the left side of the equation, you use the differentiation property:

This equation uses I_L(s) = ℒ[i_L(t)], and I₀ is the initial current flowing through the inductor.

The Laplace transform of the differential equation becomes

I_L(s)R + L[sI_L(s) – I₀] = 0

Solve for I_L(s):

For a given initial condition, this equation provides the solution i_L(t) to the original first-order differential equation. You simply perform an inverse Laplace transform of I_L(s) — or look for the appropriate transform pair in this table — to get back to the time-domain.

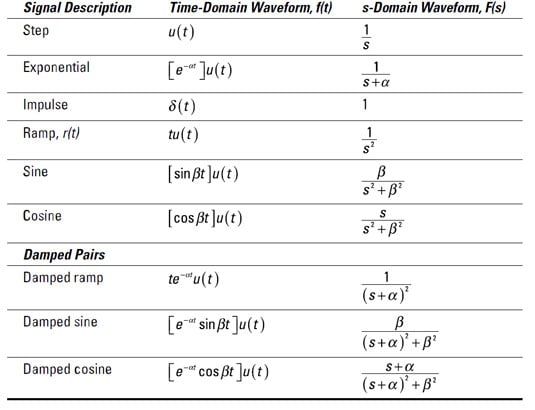
The preceding equation has an exponential form for the Laplace transform pair. You wind up with the following solution:

The result shows as time t approaches infinity, the initial inductor current eventually dies out to zero after a long period of time — about 5 time constants (L/R).