Newton’s first law says that an object remains in uniform motion unless acted on by a net force. When a net force is applied, the object accelerates. Newton’s second law details the relationship between net force, the mass, and the acceleration:
The acceleration of an object is in the direction of the net force. If you push or pull an object in a particular direction, it accelerates in that direction.
The acceleration has a magnitude directly proportional to the magnitude of the net force. If you push twice as hard (and no other forces are present), the acceleration is twice as big.
The magnitude of the acceleration is inversely proportional to the mass of the object. That is, the larger the mass, the smaller the acceleration for a given net force (which is just as you’d expect from inertia).
All these features of the relationships among net force
acceleration (a), and mass (m) are contained in the following equation:
Note that you use the term
to describe the net force because the Greek letter sigma,
stands for “sum”; therefore,
means the vector sum of all the separate forces acting on the object. If this is not zero, then there’s a net force.
You can see that the equation
is consistent with Newton’s first law of motion (which deals with inertia), because if there’s no net force
acting on a mass m, then the left-hand side of this equation is zero; therefore, the acceleration must also be zero — just as you’d expect from the first law.
If you rearrange the net-force equation to solve for acceleration, you can see that if the size of the net force doubles, then so does the size of the acceleration (if you push twice as hard, the object accelerates twice as much), and if the mass doubles, then the acceleration halves (if the mass is twice as big, it accelerates half as much — inertia):
Take a look at the hockey puck in the figure and imagine it’s sitting there all lonely in front of a net. These two should meet.
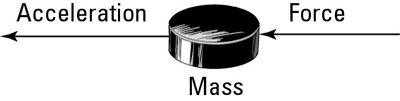
In a totally hip move, you decide to apply your knowledge of physics to this one. You figure that if you apply the force of your stick to the puck for a tenth of a second, you can accelerate it in the appropriate direction. You try the experiment, and sure enough, the puck flies into the net. Score! The figure shows how you made the goal. You applied a net force to the puck, which has a certain mass, and off it went — accelerating in the direction you pushed it.
What’s its acceleration? That depends on the force you apply (along with any other forces that may be acting on the puck), because

