One important change in the Common Core Math Standards is that students are expected to work through multi-digit computations by thinking about number relationships before they’re expected to follow standard algorithms. For parents who never had to think about their computations in school, this can make homework time a bit daunting.
For example, a subtraction method like this one went around the Internet, with people expressing horror at how complicated the Common Core makes simple arithmetic.
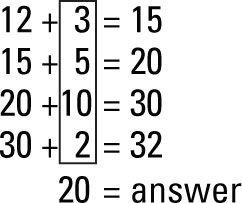
On the surface, this problem certainly does look complicated. Where does the 3 come from? What does 15 have to do with subtracting 12 from 32? Why not just do it the old-fashioned way?
If you dig a little deeper, you can see that these good questions all have reasonable answers. Children learn to count by tens and fives in kindergarten and first grade, which means that multiples of five are familiar landmarks in the number system. The 3 doesn’t magically appear; instead it’s what you need to get to 15, a multiple of five. Then you can count on by fives.
Some children may use the same sort of thinking and use 8 as their first number, which is what you need to get from 12 to 20. Adding 8 to 12 right away is another case of using a memorized fact strategically. (Here the related fact is that 2 + 8 = 10, so 12 + 8 = 20.) After the student is at 20, it’s another 10 to 30, and finally two more to get to 32. Other children may notice that 32 and 12 have the same units digit, so they may count 12, 22, 32 — two steps of ten.
Don’t mistake the fact that multiple strategies are discussed in class for a mandate that all students master all of these strategies. Teachers aren’t trying to increase the number of things students need to remember. Rather, they’re exposing students to a number of correct ways of thinking so that students can recognize and build on their own ideas.
The point of this kind of work is to help children develop addition and subtraction as related operations, not separate sets of facts to be learned. Understanding relationships among facts reduces the number of errors students make, the size of the errors they do make, and their reliance on calculators in the long run.

