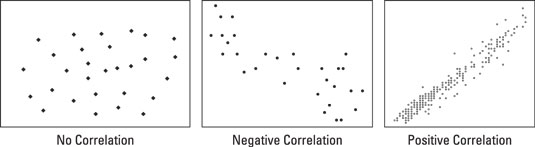
A scatter plot shows the relationship between two variables. When looking at a scatter plot, you look at the correlation, which gauges the strength of the relationship and the direction. This means a correlation can be strong or weak and can be positive, negative, or neither.
Depending on the strength of the correlation, you can infer a trend in the relationship. The figure shown here illustrates some examples of scatter plots and the types of correlations that can appear. Notice how when there is a correlation, the points tend to line up in one direction.
A common example of a scatter plot is the relationship between people’s shoe sizes and their IQs. When a large data collection is analyzed, you see that there’s no correlation. If there were one, you could make a statement like “People with bigger shoe sizes are smarter.” However, there’s a wide range of IQs and shoe size combinations, and you can’t gauge a person’s intelligence based on his or her shoe size (no correlation).
Practice question
- What statement corresponds to the relationship illustrated by the following scatter plot?
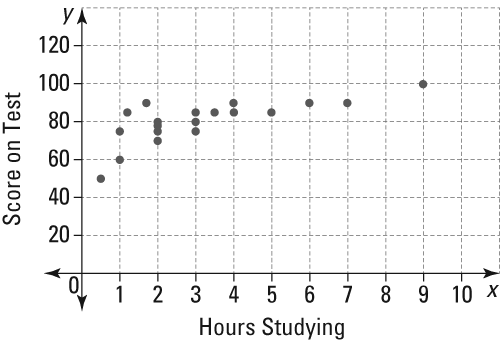
A. The longer you study, the worse you will do on the test. B. The longer you study, the better you will do on the test. C. The amount of time studying does not affect the score on the test. D. Not enough information can be gathered.
Answer and explanation
- The correct answer is Choice (B). Because the trend line, or line of best fit, of this scatter plot has a positive slope, there is a positive relationship between the variables. This means as one increases the other increases: the longer you study, the better you will do on the test, Choice (B) is correct. For there to be no relationship, the line of best fit would be a “flat” horizontal line. For a negative relationship, the slope would be negative or “pointing down.”