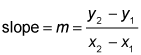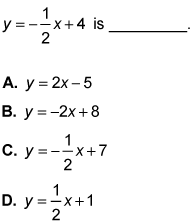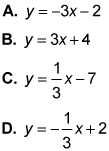In a linear function, x is usually considered to be the independent variable and y to be the dependent variable (x influences y). The independent variable (x) runs horizontally, while the dependent variable (y) runs vertically. The minimum number of points you need to construct a line is two.
The common difference of the points that describes both the steepness and direction of the line is called the slope. This is also referred to as the ratio of the rate of change in the dependent variable to the rate of change in the independent variable. The letter associated with slope is m; if m is positive, then the line rises to the right, and if m is negative, then the line falls to the right. To determine the slope of a line, you need two points: (x1, y1) and (x2, y2). Then substitute into the formula:
Slope-intercept is the most commonly used formula to represent a linear function. Just as the name implies, this formula tells you the slope (m) of the line as well as the y-intercept (b). Recall that the y-intercept is the point at which the graph crosses the y-axis.
Slope-intercept form: y = mx + b (m is the slope and b is the y-intercept)
Practice questions
Answers and explanations
- The correct answer is Choice (A).
Because you're looking for a line perpendicular to the given line, the new equation would have a negative reciprocal of the given slope:
so the new slope is m = 2. Because Choice (A) is the only equation with that slope, it is the correct answer. Choice (C) represents a line parallel to the given line, while Choices (B) and (D) have slopes that have no specific relationship with the given slope.
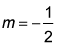
- The correct answer is Choice (A). Because you're looking for a line parallel to the given line, the new equation would have the same slope: m = –3. Because Choice (A) is the only equation with that slope, it's the correct answer. Choice (C) represents a line perpendicular to the given line, while Choices (B) and (D) have slopes that have no specific relationship with the given slope.