The Series 7 exam tests your knowledge of bond prices, bond yields, and how to calculate them. You will also need to know how accrued interest can affect how much customers have to pay for the bond.
The relationship between outstanding bond prices and yields is an inverse one. You can assume for Series 7 exam purposes that if interest rates decrease, outstanding bond prices increase and vice versa. Say, for example, that a company issues bonds with a 7-percent coupon rate for $1,000.
After the bonds are on the market, interest rates decrease. The company can now issue bonds with a 6-percent coupon rate. Investors with the 7-percent bonds are then in a very good position and can demand a premium for their bonds.
Bond yields
Below is information on the types of bond yields and how the Series 7 exam tests this topic.
Nominal yield (coupon rate)
The nominal yield (NY) is the coupon rate on the face of the bonds. For exam purposes, you can assume that the coupon rate will remain fixed for the life of a bond. If you have a 7-percent bond, the bond will pay $70 per year interest (7% × $1,000 par value). When a problem states that a security is a 7-percent bond, it’s giving the nominal yield.
Current yield
The current yield (CY) is the annual rate of return on a security. The CY of a bond changes when the market price changes; you can determine the CY by dividing the annual interest by the market price:
The following question involves bond yields.
Monique Moneybags purchased one XYZ convertible mortgage bond at 105. Two years later, the bond is trading at 98. If the coupon rate of the bond is 6%, what is the current yield of the bond?
(A) 5.7%
(B) 6.0%
(C) 6.1%
(D) Cannot be determined
The correct answer is Choice (C). This question has a lot of unnecessary information. Unfortunately, you’ll have to get used to it. The Series 7 exam creators are notorious for inserting useless (and sometimes misleading) information into the questions to daze and confuse you. In this case, you need only the annual interest and the market price to calculate the answer. Use the following formula to get your answer:

The annual interest is $60 (6% coupon rate × $1,000 par value), and the current market price is $980 (98% of $1,000 par). The facts that the bond is convertible or a mortgage bond (backed by the issuer’s property) and that it was purchased at 105 ($1,050) are irrelevant.
“Cannot be determined,” as tempting as it may be, is almost never the correct answer on the Series 7 exam.
Yield to maturity (basis)
The yield to maturity (YTM) is the yield an investor can expect if holding the bond until maturity. The YTM takes into account not only the market price but also par value, the coupon rate, and the amount of time until maturity. The formula for YTM is as follows:
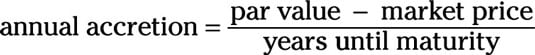
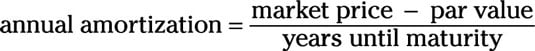
This formula can be difficult to remember. If you have it down, kudos (whatever that means) to you. It’s tested (although somewhat rarely) on the Series 7 exam, and you may be one of the unlucky blokes who need this formula.
Yield to call
The yield to call (YTC) is the amount that the investor receives if the bond is called prior to maturity. The calculations are similar to those for the YTM, but you substitute the call price for the par value. The chances of needing it on the Series 7 exam are even more remote than needing the YTM calculations.
Yield to worst
To determine the yield to worst (YTW), you have to calculate the yield to maturity and yield to call for all the call dates (if there’s more than one) and choose the lowest. If you get a question on yield to worst, knowing the definition should be enough to get you by.
Seesaw calculations for bond price and yields
Higher numbers make the seesaw rise, and lower numbers make it fall. Looking at the following diagram, you can see that if a bond is at par, the seesaw remains level. If the prices decrease, the yields increase, and if the prices increase, the yields decrease. The center support (n) represents the nominal yield of the bond because it remains constant regardless of what happens to prices or other yields.
(In the seesaw, NY stands for nominal yield, CY is current yield, YTM is yield to maturity, and YTC is yield to call.)
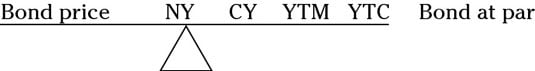
Check out the following problem and its explanation, which show you how to put the seesaw in motion.
Jonathan Bullinski purchased an 8-percent ABC bond yielding 9 percent. He purchased the bond at
(A) a discount
(B) par
(C) a premium
(D) a price that cannot be determined
The correct answer is Choice (A). The question states that the nominal yield is 8 percent and the bond is yielding 9 percent. The 9 percent is the yield to maturity:
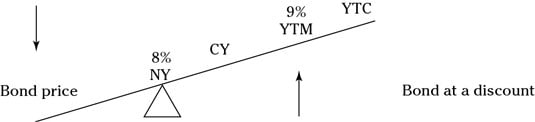
Because the YTM is greater than the NY, the right side of the seesaw goes up and the left side goes down. This means that the investor paid a price that was at a discount (below par). You can also determine that the current yield (CY) would have to be between 8 and 9 percent and the yield to call (YTC) would have to be greater than 9 percent.
If the YTM were lower than the NY, the seesaw would tip the opposite way, and the price would be at a premium rather than at a discount.

