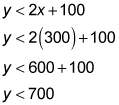The following practice questions ask you to find the minimum and maximum possible values of a y-coordinate in a given solution set.
Practice questions
- In the xy-plane, if a point with the coordinates (c, d) lies in the solution set of this system of inequalities, what is the minimum possible value of d? y > –4x + 540 y > 2x A. Slightly below 90 B. Slightly above 90 C. Slightly below 180 D. Slightly above 180
- In the xy-plane, if a point with the coordinates (e, f) lies in the solution set of this system of inequalities, what is the maximum possible value of f? y < –x + 1,000 y < 2x + 100 A. Slightly below 300 B. Slightly above 300 C. Slightly below 700 D. Slightly above 700
Answers and explanations
- The correct answer is Choice (D).
Combine the inequalities to find the (x, y) values of where the lines cross. First subtract the second inequality from the first inequality; then solve for x:
Now plug in 90 for x in the second inequality to solve for y:
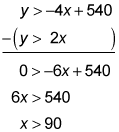 The (x, y) values of where the lines cross are (90, 180). Because each inequality has a y that's greater than the expression with the x, anything above the lines is within the solution set; d represents the y-value of where the lines cross, so the answer is slightly above 180.
The (x, y) values of where the lines cross are (90, 180). Because each inequality has a y that's greater than the expression with the x, anything above the lines is within the solution set; d represents the y-value of where the lines cross, so the answer is slightly above 180.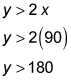
- The correct answer is Choice (C).
Combine the inequalities to find the (x, y) values of where the lines cross. First subtract the second inequality from the first inequality; then solve for x:
Now plug in 300 for x in the second inequality to solve for y:
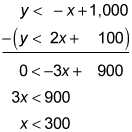 The (x, y) values of where the lines cross are (300, 700). Because each inequality has a y that's less than the expression with the x, anything below the lines is within the solution set; f represents the y-value of where the lines cross, so the answer is slightly below 700.
The (x, y) values of where the lines cross are (300, 700). Because each inequality has a y that's less than the expression with the x, anything below the lines is within the solution set; f represents the y-value of where the lines cross, so the answer is slightly below 700.