The first practice question is a simple problem (finding a labeled coordinate on a number line based on the surrounding numbers). The second question is a little trickier (finding the coordinate of a point on the line based on its distance from other points).
Practice questions
- The distance from one labeled coordinate to the next on the number line is the same in every case. What is the value of y?
A. 17.5 B. 18.5 C. 17 D. 16 E. 18
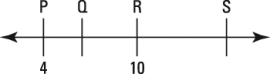
- For this number line, the distance from P to Q is half the distance from Q to R, and that distance is half the distance from R to S. The coordinate of P is 4, and the coordinate of R is 10. What is the coordinate of S?
A. 18 B. 16 C. 20 D. 24 E. 14
Answers and explanations
- The correct answer is Choice (E). The distance is the same from one labeled coordinate to the next in every case. Some of the labels indicate that each coordinate is 3 units away from the adjacent ones. The number that's 3 more than 15 and 3 less than 21 is 18.
- The correct answer is Choice (A).
You can figure out the distance from P to S if you determine the distance from P to Q, because the distance from P to S is that distance, plus twice that distance, plus twice that.
The distance from P to R is 6 because 10 – 4 = 6. Q is in a position in which its distance from P is half its distance from R. The sum of those distances is 6. Therefore, the distance from P to Q is a number that can be added to twice itself to get 6. That number is 2.
2 + 2(2) = 6
You could use algebra to determine that, but it's not necessary. Because the distance from P to Q is 2, you know that the distance from Q to R is 4 and that the distance from R to S is 8. The coordinate of P is 4, so the coordinate of S is 4 + 2 + 4 + 8, or 18.