The main parts of most of these shapes are lines and angles, so start with these.
GRE images are typically drawn close to scale, well enough for you to get a sense of what’s going on in the drawing. The drawing or the description will always tell you everything that you need (such as side lengths, parallel sides, right-angle boxes), so whether it’s drawn to scale really doesn’t factor in. You wouldn’t eyeball the answer anyway, so always look in the description for clues to unravel the drawing. On that note, if the drawing has a label that reads, “Figure not drawn to scale,” then it’s way off.
Lines
You’ve probably heard the term straight line, but in geometry, that’s redundant. By definition, a line is straight. If it curves, it’s not a line. Once in a while the GRE splits lines — er, hairs — and forces you to consider whether the line goes on forever in both directions, is a line segment, or has one endpoint and an arrow at the other end, making it a ray that goes on in one direction. But most of the time, don’t worry about it: You can usually solve the problem without worrying about how far the line goes.Parallel lines don’t cross and are represented by the symbol, Ρ. Perpendicular lines cross at right angles and are represented by the symbol
A perpendicular bisector is a line that both passes through the midpoint of a line segment and is perpendicular to it.
Angles
Angles are a common part of GRE geometry problems. An angle is the space between two lines or segments that cross or share an endpoint. Fortunately, there’s not much to understanding angles when you know the different types of angles and a few key concepts.Finding an angle is usually a matter of simple addition or subtraction. Besides the rules in the following sections, these three rules apply to the angles on the GRE:
- Angles can’t be negative.
- Angles can’t be 0 degrees or 180 degrees.
- Fractional angles, such as
degrees or 179.5 degrees, are rare on the GRE. Angles are typically whole numbers, rounded to be easy to work with. If you’re plugging in a number for an angle, plug in a whole number, such as 30, 45, or 90.
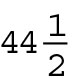
Right angle
Right angles equal 90 degrees and are represented by perpendicular lines with a small box where the two lines meet.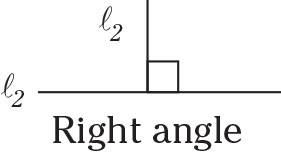
Watch out for lines that appear to be perpendicular but really aren’t. An angle is a right angle only if the description reads, “the lines (or segments) are perpendicular” or you see the box in the angle (which is the most common). Otherwise, you can’t assume the angle is 90 degrees.
Other than the words “right angle” and “bisect,” you will probably not see the following terms, so don’t worry about memorizing words such as “obtuse” or “supplementary.” But, review the definitions so that you understand how the angles work, because that’s the key to solving almost any GRE angle problem.
Acute angle
An acute angle is any angle greater than 0 degrees but less than 90 degrees.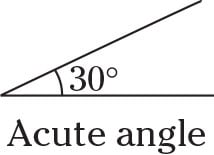
Obtuse angle
An obtuse angle is any angle greater than 90 degrees but less than 180 degrees.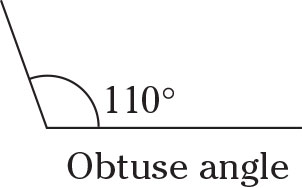
Complementary angles
Together, complementary angles form a right angle: 90 degrees.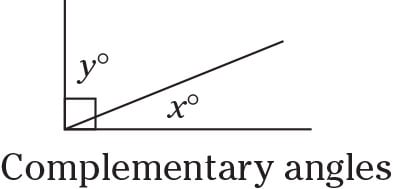
Supplementary angles
Together, supplementary angles form a straight line: 180 degrees.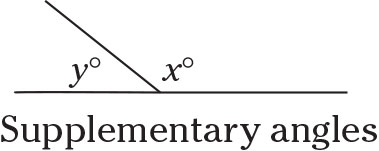
Vertical angles
Vertical angles are formed when two lines cross, and they always have equal measures.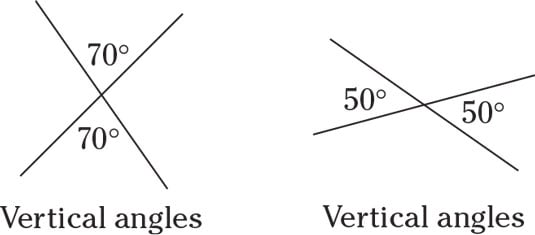
Bisectors
A bisector, or line that bisects, cuts directly down the middle, and this is a term that you need to know. Yes, more vocab. If a line (or segment) bisects an angle, it divides that angle into two equal angles; if a first segment bisects a second segment, the first one cuts the second one perfectly in half. And if the first segment bisects the second segment at 90°, then it is a perpendicular bisector as mentioned previously, and yes, the GRE will expect you to know what that is. Don’t worry though — there will almost always be a drawing.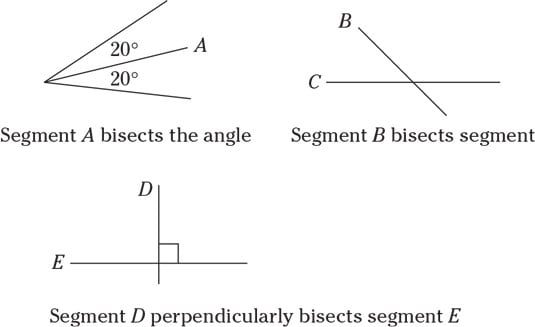
Other key points
Angles around a point total 360 degrees, just as in a circle.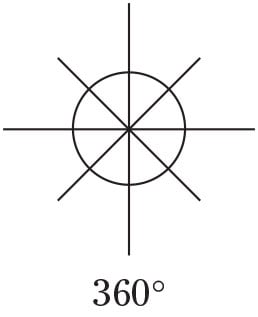
A line that cuts through two parallel lines forms two sets of four equal angles. In this drawing, all the x’s are the same, and all the y’s are the same.
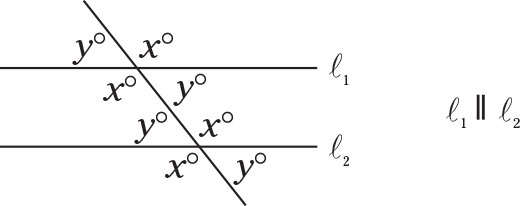
See also, "GRE Sample Math-Test Questions: Geometry," for some practice questions dealing with these concepts.

