Each Data Sufficiency problem poses a question, followed by two statements. Your task is to evaluate the statements to determine at what point there is or is not sufficient information to answer the question.
Unlike the Problem Solving questions, you do not actually have to answer the question posed. Instead, you select one of five fixed answer choices that offer different options about the sufficiency of the information provided in the two statements.
Practice questions
- A grocer sells avocados for $1.50 each and pineapples for $2.00 each. How many avocados did the grocer sell today?
(1) The number of avocados sold today is 20 more than twice the number of pineapples sold.
(2) Today the grocer received a total of $155 from the sale of avocados and pineapples.
A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
C. Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient to answer the question asked.
D. Each statement ALONE is sufficient to answer the question asked.
E. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked.
- Is the sum of the roots of the equation, x2 + bx + c = 0, positive?
(1) b < 0
(2) c < 0
A. Statement (1) ALONE is sufficient, but statement (2) alone is not sufficient to answer the question asked.
B. Statement (2) ALONE is sufficient, but statement (1) alone is not sufficient to answer the question asked.
C. Both statements TOGETHER are sufficient, but NEITHER statement ALONE is sufficient to answer the question asked.
D. Each statement ALONE is sufficient to answer the question asked.
E. Statements (1) and (2) TOGETHER are NOT sufficient to answer the question asked.
Answers and explanations
- The correct answer is C.
Let A = the number of avocados sold today, and P = the number of pineapples sold today. From (1), A = 2P +20, which is one equation with two unknowns. Without additional information, you cannot determine an exact value of A. For example, if P = 5, then A = 30. But if P = 10, then A = 40. Thus, (1) is not sufficient.
From (2), 1.50A + 2.00P = 155.00, which is one equation with two unknowns. Without additional information, you cannot determine an exact value of A. For example, if P = 1, then A = 102. But if P = 4, then A = 98. Thus, (2) is not sufficient.
Taking (1) and (2) together, yields a system of two equations, A – 2P = 20 and 1.50A + 2.00P = 155.00, with two variables, A and P. The system has a unique solution because
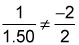
Thus, you can determine a unique value of A. Therefore, both statements together are sufficient, but neither statement alone is sufficient.
- The correct answer is A.
Using the quadratic formula, the two roots of x2 + bx + c = 0 are
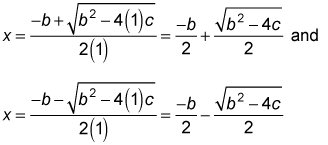
Adding the roots yields
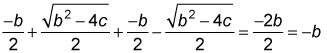
Hence, the sum of the roots of x2 + bx + c = 0 equals –b. From (1) b < 0 implies –b > 0, so the sum of the roots is positive. Thus, (1) is sufficient to answer the question posed.
From (2), c > 0 implies that the product of the two roots is negative, indicating that the two roots have opposite signs. However, without additional information, you cannot determine whether the sum is positive. For instance, the sum of the roots of x2 – 2x – 15 = 0, which has roots 3 and –5, is –2. This result yields an answer of No to the question posed. But the sum of the roots of x2 + 2x – 15 = 0, which has roots 5 and –3, is 2. This result yields an answer of Yes to the question posed. Thus, (2) is not sufficient. Therefore, statement (1) alone is sufficient.

