The following practice questions involve using measurements in different formulas to get your answers. In one case, you have to find the least expensive floor treatment for a room, and in the other, you have to use the Pythagorean theorem to find out how far a traveller is from her destination.
Practice questions
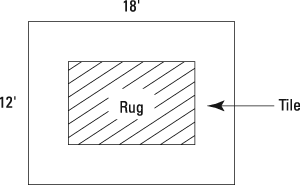
- The Symons are redecorating a room in their house. They have some interesting ideas. They want to put a rug on the floor surrounded by a border of tiles. They are considering teak paneling halfway up each wall. In addition, they may cut away part of the ceiling to put in a skylight. This is a diagram of their room:
The rug costs $7.50 a square foot, and tile costs $9.00 a square foot. One rug they like is 16 feet by 10 feet, leaving just a little area around the rug for tiles. At the store, however, they see another rug that is only 12 feet by 8 feet, but it's just the right pattern and colors for their room. Which floor treatment is less expensive?
A. both are the same cost B. the larger rug C. the smaller rug without the paneling D. the smaller rug
- Yvonne is studying a map. She is 47 miles due south of where she wants to go, but the road goes 17 miles due west to an intersection that then goes northeast to her destination. Approximately how much farther must she travel because of the way the road goes?
A. 3 miles B. 20 miles C. 16 miles D. 50 miles
Answers and explanations
- The correct answer is Choice (B).
This problem tests your measurement skills. You're asked to predict the impact of changes in the linear dimensions of the rug on its area and cost. Choice (C) seems logical, but the question never mentions the cost of the paneling or the skylight, so you can't consider it as an answer.
Draw a sketch of the room with the larger rug. It will have a tiled area around it. You have to figure out how many square feet of tile and carpet you need for this floor treatment, as follows:
The area of the room is (18)(12) = 216 square feet.
The larger rug will cover (16)(10)=160 square feet of the floor. This leaves 56 square feet (216–160) to be covered with tile. The cost of the rug is ($7.50)(160) = $1,200. The cost of the tile is ($9.00)(56) = ($504.00). The total cost is $1,200.00 + $504.00 = $1,704.00.
The smaller rug will cover (12)(8) = 96 square feet of the floor. This leaves 216 – 96 = 120 square feet to be covered with tile. The cost of the rug is ($7.50) (96) = $720.00. The cost of the tile is ($9.00)(120) = $1,080.00. The total cost is $720.00 + $1,080.00 = $1,800.00. The smaller rug will cost more for the entire floor treatment.
Tile costs more per square foot than carpeting, so you know without doing any figuring that having more tile will result in higher costs.
- The correct answer is Choice (B).
This problem is a test of your knowledge of how to use the Pythagorean theorem. Sketch out a map for this problem: Due south and due west are at right angles. So Yvonne's journey is a triangle, with the last part being the hypotenuse. Pythagoras (the guy who, as you may expect, came up with the Pythagorean theorem) said that the square of the hypotenuse of a right triangle is equal to the sum of the squares of the other two sides (a2 + b2 = c2). Thus, the square of the last leg of Yvonne's journey equals 472 + 172 = 2,498. The square root of 2,498 is 49.98. Because none of the numbers in this problem has any numbers beyond the decimal point, you can round the answer to 50. However, the question asks how much farther Yvonne must travel: She ended up traveling 17 + 50 = 67 miles and would have traveled 47 miles. Therefore, she traveled 67 – 47 = 20 miles farther.