When you’re taking the GED Mathematical Reasoning test (or any of the GED tests for that matter), you have to battle the clock. Following are ten helpful tips to save time and make sure the answers you arrive at are the correct ones.
Get real: Try to develop a sixth sense about the real world around you. Cars don’t get 160 miles per gallon, unless they’re rolling downhill, so if your answer is out of whack with reality, it’s probably wrong. Unless your test was written by an evil genius, the real-life questions should have some relationship to real life as you know it. If you come up with an answer that seems odd, check to see whether you used the correct conversion. For example, if a 10-x-15-foot room has a 120-foot ceiling, you may have mistakenly converted feet to inches.
Go with the easiest conversion: As you read the question, pay close attention to the units of measure. The units in the question should be uniform and related to the units required for the answer. If all the units are in feet and the question asks for an answer in inches, you know that you have to convert feet to inches. But what do you do if some of the answer choices are in feet and others are in inches?
If you have to convert units, choose the unit with the least chance of producing an error and the best chance of estimating the answer. If a room measures 13-x-7 yards and the answer is in feet, these numbers are easy to multiply by 3 in your head. If the room is 12.48 yards long, you would be better off using a calculator and converting at the end. Whole numbers are easier to work with than fractions or decimals.
Multiply by hundreds, tens, and ones: When multiplying a large number by a small one (single- or double-digit number), break the large number down into its component parts, multiply the parts by the smaller number, and add the results, as in the following example:
89 × 9 = (80 × 9) + (9 × 9) = 720 + 81 = 801
Round and estimate: If the answer choices you have to select from differ greatly in magnitude, you may be able to choose the correct answer without having to calculate the exact answer. When you get a question involving addition or subtraction, estimate the numbers to the nearest 5 or 10 and do the math in your head. Adding numbers that end in 5 or 0 is easier than adding numbers that end in 3 or 7, for example.
If the question specifies a maximum value, round everything up to quickly determine whether the total is less than the maximum value, as in this example:
Mary is doing some quick shopping and doesn’t want to spend more than $20.00. She buys some apples for $5.73, some grapes for $4.77, and lipstick for $6.73, plus 8% tax. Did she stay within her budget?
Round all values up to the nearest dollar and you see that $6 + $5 + $7 = $18. If tax is 8%, round it up to 10%, and you quickly see that the tax on $18 would be $1.80. $18 + $1.80 = $19.80, which is still less than $20, so you know that Mary stayed within her budget.
If the question specifies a minimum value, round all other values down first and then perform your calculations.
Skip and come back to impossibly hard questions: Keep in mind that many mathematicians are lazy people who try to solve problems the easiest way possible. If a question is becoming impossibly difficult to solve, something is usually wrong. Check over your work and make sure that you have copied all numbers correctly and that you didn’t use the wrong operation in working through the problem.
Simplify before doing the math: Before you even think about multiplying or dividing fractions or performing any series of mathematical operations, consider whether you can simplify the equation before doing the math. By simplifying, you end up with fewer and smaller numbers and may even be able to do the math in your head, saving yourself precious minutes on the test. For example, without simplifying,
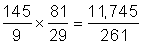
but if you simplify,
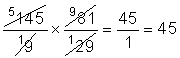
Subtract the discount percentage from one: If the problem offers you a discount of 15% from the regular price, you can either multiply the regular price by 0.15 to calculate the discount and subtract that amount from the regular price, or you can figure that if you’re getting a 15% discount, you’re paying 85% of the regular price, because
100% – 15% = 85%.
Instead of doing the problem in two steps, you do it in one and save yourself a few seconds: multiply the amount by 0.85 to get the same results in one step. You also reduce your chances of making a mistake; the more steps you take, the more chances you have of making a mistake, especially when you’re in a hurry.
Estimate fractions as zero, half, or one: When working with fractions that are less than one, ask yourself whether the fraction is closer to zero, half, or one, and then estimate your answer. Here are a couple examples:
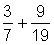
Because both fractions are close to
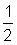
the answer is close to 1.
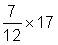
Because the fraction is just over
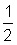
the answer is likely to be slightly more than half of 17, or slightly more than 8.5.
Add the tax or tip percentage to one: When calculating tax or tip on a total, you can calculate the tax or tip and add it to the total (two steps) or add the tax or tip percentage to 100% and multiply that by the total (one step). For example, to leave your server a 15% tip in a restaurant, you can multiply the amount on the check by 0.15 and add this to the bill to get the amount you should leave the server in total. Or you can multiply the check by 1.15 to calculate the total plus tip (100% total plus 15% tip is 115%, or 1.15). Again, fewer steps and fewer chances for error, especially if you use mental math.
Draw cards and roll dice: Many probability problems involve cards and dice, so know that a standard deck has 52 cards, 4 suits (diamonds, hearts, clubs, and spades), and 13 cards in each suit: ace, 2–10, jack, queen, and king. If you want to know your chances of drawing an ace of hearts from a full deck of cards, you know that a full deck has 52 cards and only 1 ace of hearts, so your chances are 1 in 52 of drawing an ace of hearts. If you’re happy to just draw any ace, then the deck still has 52 cards, but 4 aces, so your chances of drawing an ace are 4 in 52, or 2 in 26, or 1 in 13.
Dice questions are also common on the test. Keep in mind that every die (singular for “dice”) has 6 faces, numbered 1 to 6. Every time you roll a die, you have a 1 in 6 chance that it’ll land with a certain number facing up.

