Many of the algebra and function questions you’re up against on the PSAT/NMSQT contain exponents, raised numbers or letters. The number or letter not raised is called the base. When mathematicians talk about exponents, they call them powers, as in “six to the eighth power.”
The second power is referred to as a square, and the third power is a cube. If you have a number in front of the base, it’s called a numerical coefficient. Radicals appear here and there on the PSAT/NMSQT. You may know radicals as square roots. Some examples:
The base is 2 and the exponent is 3: 23 (also called two cubed)
The base is y and the exponent is 4: y4 (read as y to the fourth power)
The numerical coefficient is 5, the base is a, and the exponent is 2: 5a2 (read as five a squared)
The square root of 25 is 5:
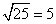
(Why 5? Because 5 x 5 = 25.)
The vocabulary doesn’t matter, but what you do with the base, exponents, and coefficients is important. Keep these rules in mind when you’re solving a PSAT/NMSQT problem with exponents or radicals:
A base with an exponent of zero equals 1. Another, more usual way to express this is base to the zero power. So 60 = 1, as does x0.
A base with an exponent of 1 equals the base. Most of the time, the 1 is simply omitted, but strictly speaking, 71 = 7 and x1 = x.
An exponent tells you how many times the base is multiplied. Therefore, a base to the second power is the base multiplied by itself. (The second power is better known as squared.) So 52 = 5 x 5 = 25. Moving on, 54 = 5 x 5 x 5 x 5 = 625.
When you’re finding a square root, look at the number under the radical and decide what was multiplied by itself to arrive at that number. If you see the following, you know that 7 x 7 = 49, so 7 is the square root of 49:
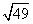
The exponent tells you how many times you have to multiply the base by itself, but the exponent isn’t what you multiply. If you see 43, you multiply 4 x 4 x 4 to get 64. You don’t multiply 4 x 3 to get 12.
Exponents can be negative numbers or fractions. A negative exponent flips the base by creating a reciprocal, 1 over the base. So x–3 is the reciprocal of x3, which you can write as
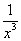
In fractional exponents, the fraction’s denominator tells you which root or radical to apply to the base. So
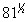
is asking for the square root of 81, or 9. Another example:
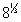
is 2 because you’re finding the cube root of 8.
Your calculator is a good friend when you’re working with powers. Use either the yx button or the ^ button. Just type the base, then the exponent, then the equal-sign button and you’re done! Most calculators can also handle fractional powers. Enter ^ before the fraction, and then enter the fraction.
Be sure to place the fraction in parenthesis! If you forget the parenthesis, you get the wrong answer. On some calculators, you press the second function key to find a root in this form:
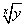
To multiply like bases, add the exponents. To divide like bases, subtract the exponents. So y5 x y4 = y9 and y5 ÷ y2 = y3.
Don’t even think about applying the preceding rule to unlike bases. Nope. Never. Not gonna happen! You have to factor it out or deal with it as it is.
For an exponent inside and outside a parenthesis, multiply the exponents. So (53)2 = 56 and (7x)5= 75x.
To add or subtract, both the bases and the exponents must match. You can’t add 62 and 83, nor can you subtract 2x4 from 4x3. However, you can deal with addition and subtraction if the bases and powers match. When everything matches, all you have to do is add or subtract the coefficients (the numbers in front of the base).
Here’s a legal problem and solution: 2x2 + 5x2 = 7x2. One more example, this time with subtraction: 9y3 – y3 = 8y3. Did you notice that 1 was subtracted from 9, even though no 1 appears in the question? The 1 in front of the y3 is understood because 1 of anything is itself.
Power to the people! Now that your head is filled with exponent rules, try these problems.
Simplify: (x2)3x3
(A) x3
(B) x8
(C) x9
(D) x12
(E) x18
The expression 2a3a can be written as
(A) 5a
(B) 52a
(C) 6a
(D) 62a
(E) 6a2
Simplify:
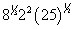
(A) 5
(B) 40
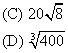
(E) 400
Now check your answers:
C. x9
PEMDAS to the rescue once again! First you want to cube x2, so you get x6x3, and then you add the exponents together now that you have the same base: x9, or Choice (C).
C. 6a
In this case you have a copies of 2 and a copies of 3, so you can think of each copy of 2 matching up with a copy of 3 and multiplying to make 6. You end up with a copies of 6, or Choice (C).
B. 40
Take each term by itself, simplify it, and then multiply everything together. First,
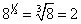
Next, 22 = 4, no problem. Finally,
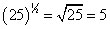
Now, just multiply the three results together: 2 x 4 x 5 = 40. Choice (B) it is!

