Not every algebra problem on the PSAT/NMSQT is an equation. You may need to find out what happens to one quantity when it varies directly or inversely in relation to another quantity. No sweat. You already know how to solve these problems.
Direct variation questions are just ratios in disguise. To solve a problem in which two quantities (say, a and b) vary directly, remember that the ratio of a to b is a constant. (Which constant? That’s probably what the question wants you to find out.) Set up a ratio with the original values of a and b marked with the subscript 1 and the new values marked with a 2:
Now you can cross-multiply and solve. Here’s the ratio for this question: At Adam’s party, the number of balloons inflated (12) varied directly with the number of balloons popped before the party even began (8). How many balloons will pop before Adam’s next party if he inflates 36 balloons?
Okay, call the balloons inflated a1 and the balloons popped b1. So a1 is 12 and b1 is 8. Your ratio is then
When you cross-multiply, you get
288 = 12b2
Now divide each side of the equation by 12, and you get 24 = b2. Your answer is 24 deflated, garbage-ready balloons.
Notice that when one variable increases, the other variable does too. You can eliminate some choices quickly if you remember this fact about direct variation.
Now for inverse variation. Here the product of the two variables (say, a and b) is always the same number, or constant. So if a = 7 and b = 9, the constant is 7 x 9 or 63. So if a is 3, b must be 21, because 3 x 21 = 63.
If the number of balloons destroyed by ripping or puncturing before the party varies inversely, Adam may lose 7 to rips and 9 to punctures, or 3 to rips and 21 to punctures. Either way his party will be lacking in decorations.
Try these practice questions:
The number of word problems a math teacher assigns varies directly with the number of questions she is asked during class. She assigned 6 word problems on Monday after 15 questions were asked. If 20 questions were asked on Wednesday, how many word problems did she assign?
(A) 4
(B) 6
(C) 8
(D) 10
(E) 15
The values of p and q vary inversely. When p has a value of 8, q has a value of 10. What is the value of p when q is 4?
(A) 2
(B) 5
(C) 10
(D) 20
(E) 40
Now check your answers:
C. 8
Remember, direct variation means that the ratio is constant, so set up an equation:
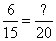
You can either cross-multiply to solve or see that the first fraction reduces down to 2/5, meaning that for every 5 questions, the teacher assigns 2 word problems. This means that when the teacher hears 20 questions (4 x 5), she’ll assign 4 x 2 = 8 word problems, Choice (C).
D. 20
When you’re dealing with variables that vary inversely, always remember that multiplication is the key. No matter what p and q are, they should always multiply to the same value. The given values, 8 and 10, multiply to 80, so all p-q pairs should multiply to 80. When q is 4, p must be (80 / 4) = 20, Choice (D).

