Mixture problems on the ASVAB often involve mixing different items at different costs and determining the final cost of the mixture. They can also involve mixing various solutions and determining percentages of the solution mixture. This concept sounds difficult, but it’s really pretty easy when you know how. Are you ready to try a couple?
How many quarts of a 70-percent alcohol solution must be added to 50 quarts of a 40-percent alcohol solution to produce a 50-percent alcohol solution?
Let x = the number of quarts of 70-percent solution needed. The amount of alcohol contained in x quarts of the 70-percent solution is represented by 0.7x.
You have 50 quarts of the 40-percent solution, so the amount of alcohol contained in those 50 quarts is represented by 50 × 0.4 = 20 quarts.
The total number of quarts of solution can be represented as 50 + x (the number of quarts of 40-percent solution plus the unknown number of quarts of 70-percent solution). Half (50 percent) of that solution will be alcohol, so 0.5(50 + x).
| Quarts of Solution | Percent Alcohol (as Decimal) | Total Quarts of Alcohol | |
|---|---|---|---|
| 70% solution | x | 0.7 | 0.7x |
| 40% solution | 50 | 0.4 | 0.4 × 50 = 20 |
| 50% solution | 50 + x | 0.5 | 0.5(50 + x) |
The fourth column gives you your equation: 0.7x + 20 = 0.5(50 + x). First, distribute the 0.5 to the terms in parentheses. Then work the equation as follows:
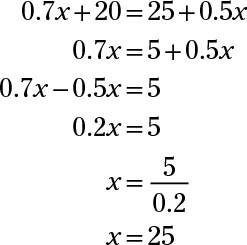
The final mixture will require 25 quarts of 70-percent solution.
A grocery store wants to offer a mixture of green and red grapes to sell for $4.20 per pound. If green grapes cost $3 per pound and red grapes retail for $6 per pound, how many pounds of red grapes should the grocer add to 12 pounds of green grapes to produce the desired mixture?
Let x = the pounds of red grapes. The total amount of grapes will be the pounds of green grapes (12) plus the unknown pounds of red grapes (x), or 12 + x. The total cost of green grapes at $3 per pound is 12 · 3 = $36.
Red grapes sell for $6 per pound, so their total cost is represented as 6x.
The total cost of the mixture is to be $4.20 per pound, so you can represent it as 4.2(12 + x).
Again, the last column gives you your equation: 36 + 6x = 4.2(12 + x). First, distribute the 4.2 to the terms in parentheses. Then work the equation as follows:
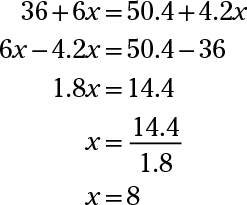
Don’t forget the information here to finish off the problem.
| Type | Cost per Pound | Pounds | Total Cost |
|---|---|---|---|
| Green | $3 | 12 | $3 × 12 = $36 |
| Red | $6 | x | $6x |
| Mixture | $4.20 | 12 + x | $4.20(12 + x) |
The mixture will require 8 pounds of red grapes.

