Pulleys and gears are simple machines that you need to know for the ASVAB Mechanical Comprehension subtest. They can be used to change the magnitude and direction of force. When you ride in an elevator, step onto an escalator, drive your car, or wind your watch, you’re using pulleys and gears.
Block and tackle systems
When used in a block and tackle arrangement, pulleys make lifting heavy objects easier. In block and tackle systems, pulleys can also be used to change the direction of your pull. If you tie a 200-pound crate to one end of a rope, run the rope through a pulley, and grab the other end of the rope, you can pull down on the rope to lift the crate up.
Without a pulley, you could pull down on the crate all day, and it wouldn’t go up. In this case, using a simple pulley, the force of your pull must equal the weight of the object being lifted. The regular pulley doesn’t multiply your force, but it makes the process of lifting easier.
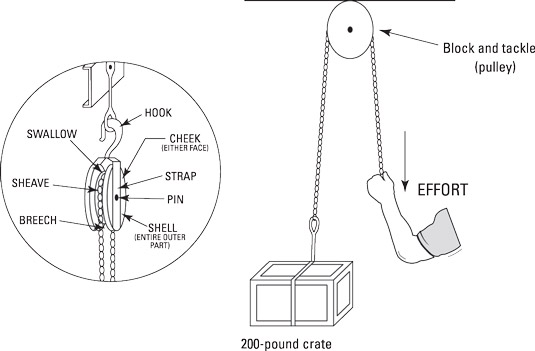
Using a block and tackle allows you to distribute your force more effectively. Instead of hoisting that entire 200-pound crate in one try, you can pull on a rope to lift it a few inches at a time. This makes the work easier to perform.
A block and tackle system can also be used to reduce effort by magnifying force:
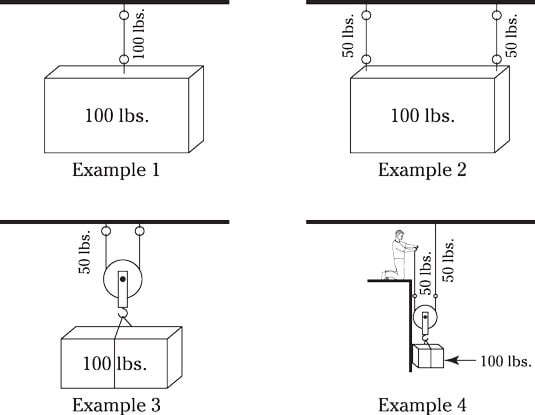
Example 1 shows a 100-pound box secured to the ceiling by a single line. The weight supported by the line is equal to the weight of the box.
In Example 2, the box is secured to the ceiling by using two lines. Each line is supporting one-half the weight of the box.
In Example 3, a single line is threaded through a pulley. Although the line is supporting the entire weight of the box, each section of the line is supporting only one-half of the box’s weight, just as in Example 2.
In Example 4, a man is using this principle to lift the 100-pound box by applying only 50 pounds of force. In short, this block and tackle system provides the man with a mechanical advantage of 2. In this example, the man would have to pull 2 feet of rope to raise the box 1 foot.
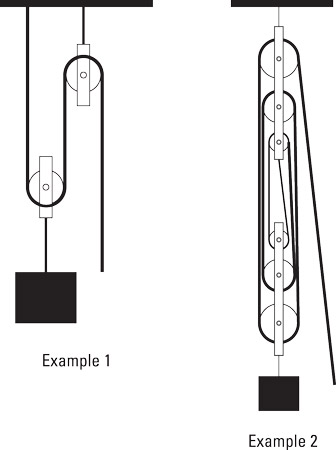 Two examples of a block and tackle arrangement.
Two examples of a block and tackle arrangement.In Example 1, three sections of rope produce a mechanical advantage of 3. Lifting a weight with this pulley arrangement requires only of the effort required to lift the weight directly. However, in order to lift the crate 1 foot, you have to pull 3 feet of rope.
Example 2 illustrates a block and tackle system with six sections of rope. Using this arrangement provides you with a mechanical advantage of 6, but you have to pull the rope 6 feet for every foot you want to raise the box.
Understanding how gears work
Machines often use gears to transmit motion from one place to another. An additional advantage of using gears is that they can be used to change direction, increase or decrease speed, or increase or decrease force.
Gears arranged in a series turn in the opposite direction of each other. If you have an even number of gears connected in a series, the first and last gear turn in opposite directions. If you have an odd number of gears aligned in a series, the first and last gear spin in the same direction.
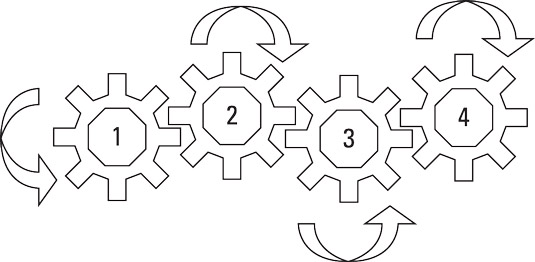
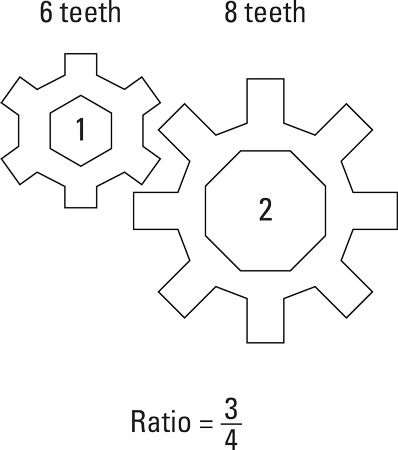
The speed at which a gear rotates depends on the number of teeth. Gear 1 has six teeth, and Gear 2 has eight teeth. This relation of teeth can be expressed as a ratio of 6:8, which can be reduced to 3:4. That means Gear 1 has to rotate four times in order for Gear 2 to make three revolutions. Or expressed another way, for each rotation made by Gear 1, Gear 2 will make three-quarters of a revolution.
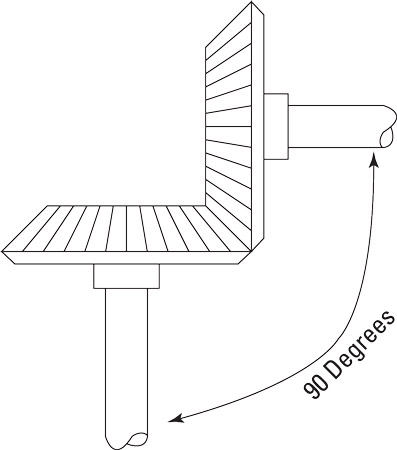
When gear shafts aren’t parallel to one another, bevel gears can be used to connect gears that have shafts at different angles. The principles of gear rotation remain the same. Here’s an example of bevel gears designed to connect shafts having a 90-degree angle to the other.
Pulley and belt arrangements
When connected by a system of belts, pulleys can also drive other pulleys.
Like gears, pulleys are used to transmit motion from one location to another. However, the physical properties of pulleys are different from those of gears:
Turning direction: Unless the driving belt is reversed, pulleys connected in series rotate in the same direction. This concept is illustrated below with two sets of pulleys. In the first set of pulleys, all the pulleys turn in the same direction as the driving pulley. However, in the second set of pulleys, the driving pulley and the lower pulley are rotating counterclockwise, but the right-hand pulley is rotating in a clockwise direction because the belt is twisted.
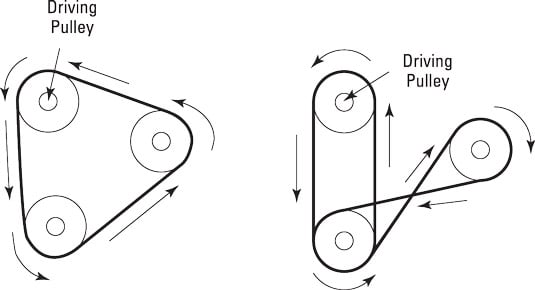 Pulleys rotate in the same direction unless the belt is reversed.
Pulleys rotate in the same direction unless the belt is reversed.Speed of rotation: Although the speed of gear rotation is determined by the number of teeth, how fast a pulley rotates depends on the diameter of the pulley in relation to the diameter of the pulley that’s driving it.
Have a look below. Pulley A has a diameter of 1 inch, Pulley B has a diameter of 2 inches, and Pulley C measures 4 inches in diameter. The ratio among the three pulleys is 1:2:4. For every complete revolution made by Pulley A, Pulley B makes half of a revolution. Each time Pulley B makes a full revolution, Pulley C makes half of a revolution. Thus, for every full revolution of Pulley A, Pulley C makes a quarter of a revolution.
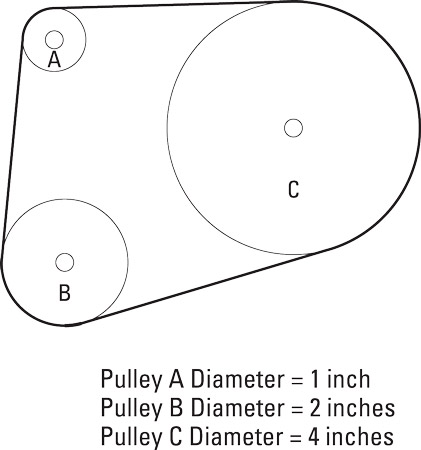 Pulleys in action.
Pulleys in action.

