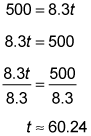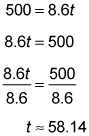Practice questions
- Captain Mike leaves the dock at 10:00 a.m. and travels down the calm river in his boat at 55 miles per hour. How far will he have traveled by 5:00 p.m.?
A. 330 miles B. 275 miles C. 380 miles D. 385 miles
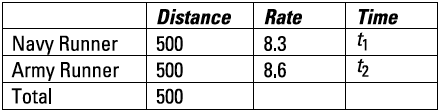
- An Army team and a Navy team are running a relay race with participants stationed 500 meters apart. The first runner from each team starts from the same point at the same time. The Army runner runs at 8.6 miles per hour, and the Navy runner runs 0.3 miles per hour slower than the Army runner does. How much sooner will the Army runner reach her team's second participant than the Navy runner will?
A. 2.5 seconds B. 3 seconds C. 2.1 seconds D. 2.7 seconds
Answers and explanations
- The correct answer is Choice (D).
To find out how far Captain Mike has traveled, let t represent the number of hours he's been on the go. Use the distance formula, d = rt, where d represents distance, r represents rate (speed), and t represents time. You know that Captain Mike leaves the dock at 10 a.m. and is traveling until 5:00 p.m., so he's on the move for 7 hours.
d = rt = 55(7) = 385
After 7 hours, Captain Mike has logged 385 miles in his boat.
- The correct answer is Choice (C).
This is a classic distance word problem that you can solve by using the distance formula, which is d = rt, with d representing distance, r representing rate (speed), and t representing time.
Create a table that shows you how to set up your equations:
Distance equals rate times time, so use the formula for each runner to find out how quickly she'll reach her team's second participant over a 500-meter distance.
Navy runner:
Army runner:
Remember that the problem wants to know how much sooner the Army runner will reach her team's second participant, so subtract the Army runner's time from the Navy runner's time:
60.24 – 58.14 = 2.1
The Army runner will reach her team's second participant 2.1 seconds before the Navy runner will.