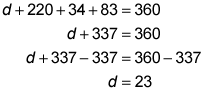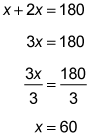Practice questions
- Find angle D in a quadrilateral where angle A measures 220 degrees, angle B measures 34 degrees, and angle C measures 83 degrees.
A. 50 degrees B. 34 degrees C. 23 degrees D. 18 degrees
- The measure of one supplementary angle, A, is twice the measure of its counterpart, angle B. What is the measure of angle A?
A. 60 degrees B. 90 degrees C. 120 degrees D. 150 degrees
Answers and explanations
- The correct answer is Choice (C).
All the angles in a quadrilateral must add up to 360 degrees, so you can subtract each of the angles from 360 to find out what's left:
360 – 220 – 34 – 83 = 23.
If you're more comfortable with algebra, you can set up an algebraic equation:
Either way, you find that the missing angle, D, is 23 degrees.
- The correct answer is Choice (C).
Supplementary angles must add up to 180 degrees. Let x represent the measure of angle B (the smaller angle) and let 2x represent the measure of angle A. Create an equation:
Angle B measures 60 degrees, so the measure of angle A is twice that; it's 120 degrees.