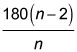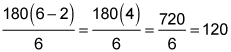Fortunately, as you'll see in the following practice questions, there's a handy formula that you can use to find a missing interior angle in a polygon, whether it's a square, a hexagon, or whatever.
Practice questions
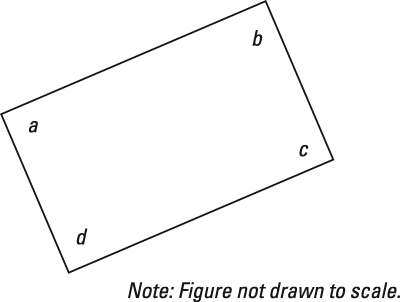
- In the figure, the following is true about the value of the degree measurement of angles a and b: 70 < a + b < 150. Which of the following describes all possible values in degrees of c + d?
A. 210 < c + d < 290 B. 30 < c + d < 110 C. 120 < c + d < 200 D. 390 < c + d < 470 E. 570 < c + d < 650
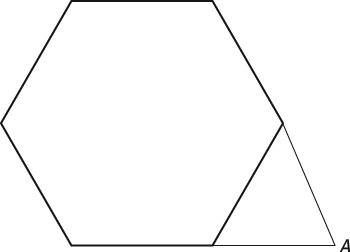
- The regular polygon shown here has 6 congruent sides and 6 congruent interior angles. Two of the sides are extended until they meet at point A. What is the measure of angle A?
A. 160 degrees B. 120 degrees C. 72 degrees D. 60 degrees E. 35 degrees
Answers and explanations
- The correct answer is Choice (A).
To find the sum of the interior angles of a polygon, you use this formula:
where n is the number of sides in the polygon.
If you can't remember that formula, simply divide the shape into triangles. The sum of the interior angles in each triangle measures 180 degrees, so for each triangle add 180 degrees and you get the sum of all the angles in the polygon.
The polygon in this problem has 4 sides, so you know its interior angles add up to 360 degrees. The problem tells you that the sum of angles a and b is more than 70 degrees. The lowest possible value for a + b is 71 degrees. If
at its lowest, then
at its highest. That means that
The answer that states c + d < 290 is Choice (A).
Double-check the rest of the information to make sure Choice (A) is the right answer. The problem says that a + b < 150. If a + b < 150, then its highest value is 149 degrees; the lowest the sum of c and d can be is 360 – 149 = 211. Choice (A) works.
- The correct answer is Choice (D).
The formula for finding the interior angle measures of a regular polygon is as follows, where n represents the number of sides in the polygon:
Apply the formula to the figure in the question to find the measure of each interior angle in the polygon:
So each angle in the hexagon measures 120 degrees. The angles in the triangle that's formed by the two extended sides must each be 60 degrees because two of those angles form a straight line with the two 120-degree angles in the hexagon and 180 – 120 = 60. If two angles in a triangle each measure 60 degrees, the third angle, angle A, must also measure 60 degrees.