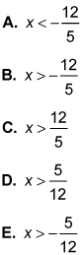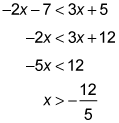Practice questions
- Given that x is an integer, for what value of x is
and x + 4 < 16?
A. 7 B. 8 C. 10 D. 12 E. 13
- Which of the following represents all possible solutions for x in the inequality –2x – 7 < 3x + 5?
Answers and explanations
- The correct answer is Choice (C).
Instead of working out complex calculations, first examine the answer choices. Based on the second equation, you can eliminate Choices (D) and (E). Neither 13 + 4 nor 12 + 4 is less than 16.
Then plug the remaining options into the first equation. Because you're determining which answer results in a value greater than 16, start with the greatest value, 10.
If x is 10 in the first expression, then
which is certainly more than 16. The first equation is valid.
Try the second: 10 + 4 < 16. This inequality is also true, so the answer must be Choice (C).
You can try the other options, but neither x = 7 nor x = 8 results in a value greater than 16.
- The correct answer is Choice (B).
Solve the inequality just as you would an ordinary equation. Move all the constants to the right and all the x terms to the left:
Choice (B) is the answer.
Choice (A) is wrong because you must change the direction of the sign when you divide both sides of an inequality by a negative value.