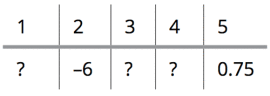
Practice questions
- What is the fourth term of the geometric sequence whose second term is –6 and whose fifth term is 0.75?
A. –3 B. –1.5 C. –0.5 D. 1.5 E. 3
- Which of the following would express the 21st term of the geometric sequence represented by 3, 9b, 27b2…?
A. (3b)21 B. 321b20 C. 320b21 D. 3b20 E. 9b21
Answers and explanations
- The correct answer is Choice (B).
Create the number sequence with the information you're given:
Because the sequence is geometric, you multiply by the same value to find each term. The second term is negative and the fifth is positive, so you must be multiplying by a negative value. Therefore, the fourth term must be negative and you can eliminate Choices (D) and (E).
You could spend time determining the common ratio between each term, but it's likely faster to try out the remaining answer choices. If the fourth term is Choice (C), –0.5, the common ratio would be –15 because 0.75 divided by –0.5 is –15. When you multiply –6 by –15, you get 90 for the third term and –1,350 for the fourth term, so Choice (C) doesn't work.
When you apply Choice (B), you have a fourth term of –1.5. Divide 0.75 by –1.5 to find the common ratio:
If –0.5 is the common multiplier, the third term would be 3:
The fourth term would be –1.5:
That works, so the fourth term must be –1.5, Choice (B).
- The correct answer is Choice (B).
Because the first number in this series is 3 and the next values are 9b and 27b2, the common multiplier in the geometric series is 3b. The first term in the series is 3. To reach the 21st term, you need to find 20 additional terms multiplied by 3b: 3(3b)20. Expand (3b)20 to
and combine terms by adding the exponents:
The correct answer is Choice (B).
Choice (A) would make sense if the first term were 3b instead of 3.