In the following practice questions, you're asked to find an average of averages and then use a stem and leaf plot to find the median cookie sales for a scout troop.
Practice questions
- A statistician for a baseball team calculated that the average batting-average for the 9 starters is 0.252, and the average batting-average for the 11 reserves is 0.225. What is the average batting-average for the whole team?
A. 0.23625
B. 0.23715
C. 0.23850
D. 0.23050
E. 0.24020
The following stem and leaf plot shows the number of boxes of cookies sold by 22 members of a Tiger Scout troop.
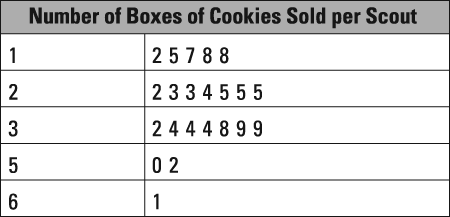
- What was the troop's median number of cookie boxes sold? A. 24 B. 25 C. 25.5 D. 26 E. 32
Answers and explanations
- The correct answer is Choice (B).
Write out the average formula:
and fill in what you know. You can find the sum of the starters' averages by completing the formula:
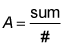 You can find the sum of the reserves in the same way:
You can find the sum of the reserves in the same way: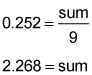 Use the average formula once more to find the batting average for all 20 team members:
Use the average formula once more to find the batting average for all 20 team members: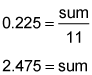
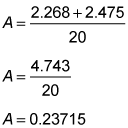
- The correct answer is Choice (B). This stem and leaf plot presents a set of values in terms of their tens and ones digits. The left column is the tens digit, and the right column is the ones digit for each of the numbers of cookie boxes sold. The median of a set of even numbers is the average of the two middle values. In this set of 22 values, the middle values are the 11th and 12th values. Count the first 10 leaves in the stem and leaf plot. The next two values are both 25, so the median value is 25.

