Practice questions
- Given that –|3 – 3a| = –12, which of the following could be a?
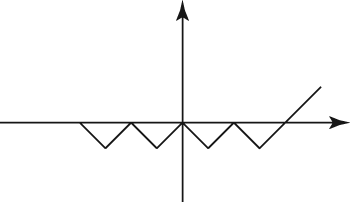
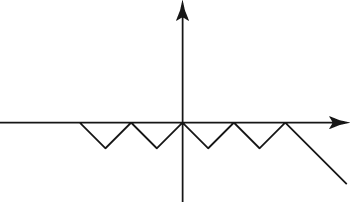
A. 5 B. 4 C. 3 D. 2 E. 1 The following figure shows the graph of y = |f (x)|.
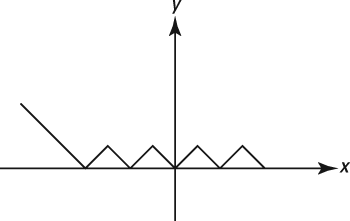
- Which of the following could be the graph of y = f (x)?
Answers and explanations
- The correct answer is Choice (A).
The straight lines indicate absolute value, which is always positive. Therefore, 3 – 3a must equal 12 or –12. For 3 – 3a = 12, a = –3, which is not one of the answer choices. For 3 – 3a = –12, a = –5, which is Choice (A). If you chose Choice (C), you forgot to change the sign when you moved the 3 to the other side of the equal sign.
You can also take a simple shortcut by plugging in the answer choices. The ACT is nice enough to give you the answer for each problem; all you have to do is substitute each answer choice to see which one could be a value for a.
- The correct answer is Choice (E).The key to solving this problem is knowing the definition of absolute value. The absolute value of a number is simply its absolute distance from zero (like on a number line) and will always be positive.
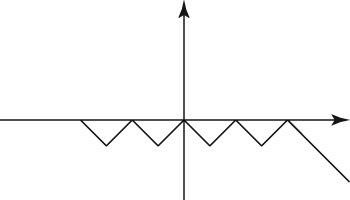
This figure, then, is the positive version of whatever makes up f(x). You have to figure out just exactly what that whatever is. There are several possibilities, but a correct answer will have the same basic pattern as the original. It will just be reflected below the x-axis.
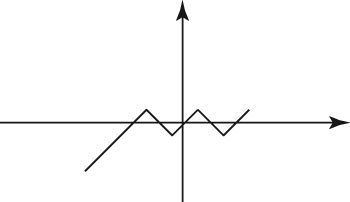
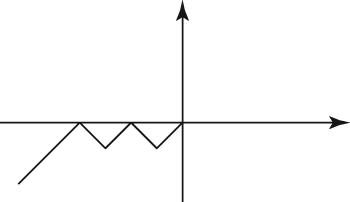
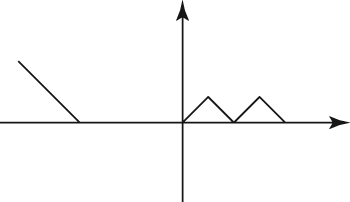
Eliminate answers that can’t be right. Choice (D) disconnects the straight line from the rest of the graph. It doesn’t maintain the same general pattern as the original, so it’s wrong. Choices (B) and (C) eliminate two of the four original zigzags, so they can’t be right. Choice (A) has the proper number of zigzags, but the straight line goes off in the wrong direction, across the x-axis. The only answer that shows a representation of the pattern of the original figure reflected below the x-axis is Choice (E). It provides the mirror image of the original pattern below the x-axis, and the original could be the absolute value (positive version) of this pattern.