set.vers? R programmers know the answer: not many. In fact, here’s vers.virg, the two-thirds of the irises that aren’t setosa:vers.virg <- subset(iris, Species !="setosa")
This image shows the plot of Petal.Width versus Petal.Length for this data frame. You can clearly see the slight overlap between species, and the resulting nonlinear separability.
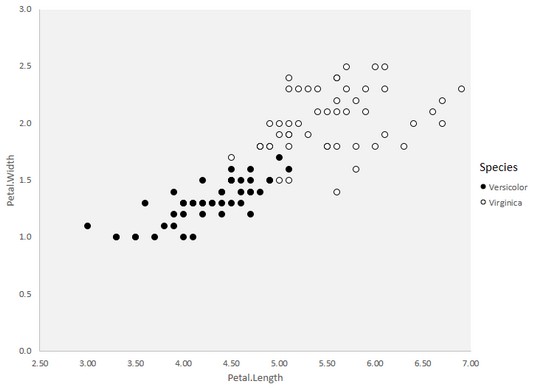
Petal.Width versus Petal.Length in the vers.virg data frame, showing nonlinear separability.How can a classifier deal with overlap? One way is to permit some misclassification — some data points on the wrong side of the separation boundary.
You may have eyeballed a separation boundary with the versicolor on the left and (most) virginica on the right. The image shows five virginica to the left of the boundary. This is called soft margin classification.
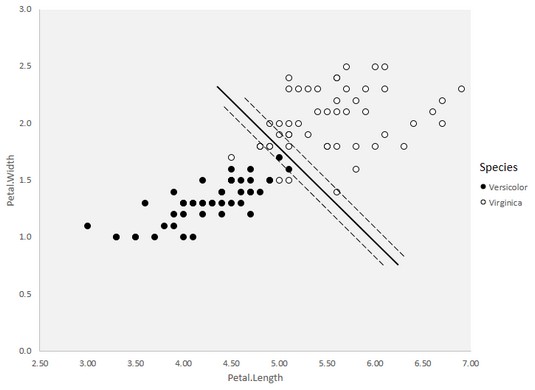Soft margin classification in the vers.virg data frame.As you eyeball the boundary, you should try to minimize the miscalculations. As you examine the data points, perhaps you can see a different separation boundary that works better — one that has fewer misclassifications, in other words. An SVM would find the boundary by working with a parameter called C, which specifies the number of misclassifications the SVM is willing to allow.
Soft margin classification and linear separability, though, don’t always work with real data, where you can have all kinds of overlap. Sometimes you find clusters of data points from one category inside a large group of data points from another category. When that happens, it’s often necessary to have multiple nonlinear separation boundaries, as shown below. Those nonlinear boundaries define a kernel.
An SVM function typically offers a choice of several ways to find a kernel. These choices have names like “linear,” “radial,” “polynomial,” and “sigmoid”.
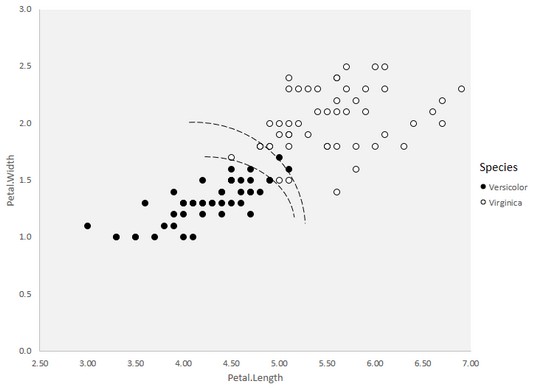A kernel in the vers.virg data frame.The underlying mathematics is pretty complicated, but here’s an intuitive way to think about kernels: Imagine the first image above as a page torn from this book and lying flat on the table. Suppose that you could separate the data points by moving them in a third dimension above and below the page — say, the versicolor above and the virginica below. Then it would be easy to find a separation boundary, wouldn’t it?
Think of kerneling as the process of moving the data into the third dimension. (How far to move each point in the third dimension? That’s where the complicated mathematics comes in.) And the separation boundary would then be a plane, not a line.