Getting to Know the Limits of Bias in Machine Learning

When you make a machine learning algorithm work on data in order to guess a certain response, you are effectively taking a gamble, and that gamble is not just because of the sample you use for learning. There’s more. For the moment, imagine that you freely have access to suitable, unbiased, in-sample data, so data is not the problem. Instead you need to concentrate on the method for learning and predicting.

For instance, you can’t fully determine the behavior of human beings by knowing their previous history and behavior. Maybe a random effect is involved in the generative process of our behavior (the irrational part of us, for instance), or maybe the issue comes down to free will (the problem is also a philosophical/religious one, and there are many discordant opinions). Consequently, you can guess only some types of responses, and for many others, such as when you try to predict people’s behavior, you have to accept a certain degree of uncertainty which, with luck, is acceptable for your purposes.

Second, you must consider that you’re betting that the relationship between the information you have and the response you want to predict can be expressed as a mathematical formula of some kind, and that your machine learning algorithm is actually capable of guessing that formula. The capacity of your algorithm to guess the mathematical formula behind a response is intrinsically embedded in the nuts and bolts of the algorithm.

Some algorithms can guess almost everything; others actually have a limited set of options. The range of possible mathematical formulations that an algorithm can guess is the set of its possible hypotheses. Consequently, a hypothesis is a single algorithm, specified in all its parameters and therefore capable of a single, specific formulation.

Mathematics is fantastic. It can describe much of the real world by using some simple notation, and it’s the core of machine learning because any learning algorithm has a certain capability to represent a mathematical formulation. Some algorithms, such as linear regression, explicitly use a specific mathematical formulation for representing how a response (for instance, the price of a house) relates to a set of predictive information (such as market information, house location, surface of the estate, and so on).

Some formulations are so complex and intricate that even though representing them on paper is possible, doing so is too difficult in practical terms. Some other sophisticated algorithms, such as decision trees, don’t have an explicit mathematical formulation, but are so adaptable that they can be set to approximate a large range of formulations easily. As an example, consider a simple and easily explained formulation. The linear regression is just a line in a space of coordinates given by the response and all the predictors. In the easiest example, you can have a response, y, and a single predictor, x, with a formulation of

y=β₁x₁ + β₀

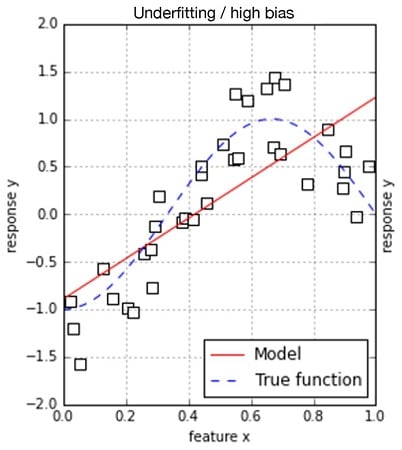
In a simple situation of a response predicted by a single feature, such a model is perfect when your data arranges itself as a line. However, what happens if it doesn’t and instead shapes itself like a curve? To represent the situation, just observe the following bidimensional representations.

Example of a linear model struggling to map a curve function.

When points resemble a line or a cloud, some error occurs when you’re figuring out that the result is a straight line; therefore the mapping provided by the preceding formulation is somehow imprecise. However, the error doesn’t appear systematically but rather randomly because some points are above the mapped line and others are below it. The situation with the curved, shaped cloud of points is different, because this time, the line is sometimes exact but at other times is systematically wrong. Sometimes points are always above the line; sometimes they are below it.

Given the simplicity of its mapping of the response, your algorithm tends to systematically overestimate or underestimate the real rules behind the data, representing its bias. The bias is characteristic of simpler algorithms that can’t express complex mathematical formulations.