Understanding the purpose of data mapping
The main idea behind data mapping is to apply a function to all members of a list or similar structure. Using mapping can help you adjust the range of the values or prepare the values for particular kinds of analysis. Functional languages originated the idea of data mapping, but mapping now sees use in most programming languages that support first-class functions.The goal of mapping is to apply the function or functions to a series of numbers equally to achieve specific results. For example, squaring the numbers can rid the series of any negative values. Of course, you can just as easily take the absolute value of each number. You may need to convert a probability between 0 and 1 to a percentage between 0 and 100 for a report or other output. The relationship between the values will stay the same, but the range won’t. Mapping enables you to obtain specific data views.
Performing data mapping tasks with Haskell
Haskell is one of the few computer languages whosemap function isn't necessarily what you want. For example, the map associated with Data.Map.Strict, Data.Map.Lazy, and Data.IntMap works with the creation and management of dictionaries, not the application of a consistent function to all members of a list (see this Haskell example for details). What you want instead is the map function that appears as part of the base prelude so that you can access map without importing any libraries.The map function accepts a function as input, along with one or more values in a list. You might create a function, square, that outputs the square of the input value: square x = x * x. A list of values, items = [0, 1, 2, 3, 4], serves as input. Calling map square items produces an output of [0,1,4,9,16]. Of course, you could easily create another function: double x = x + x, with a map double items output of [0,2,4,6,8]. The output you receive clearly depends on the function you use as input (as expected).
You can easily get overwhelmed trying to create complex functions to modify the values in a list. Fortunately, you can use the composition operator (., or dot) to combine them. Haskell actually applies the second function first. Consequently, map (square.double) items produces an output of [0,4,16,36,64] because Haskell doubles the numbers first, and then squares them. Likewise, map (double.square) items produces an output of [0,2,8,18,32] because squaring occurs first, followed by doubling.
The apply operator ($) is also important to mapping. You can create a condition for which you apply an argument to a list of functions. As shown below, you place the argument first in the list, followed by the function list (map ($4) [double, square]). The output is a list with one element for each function, which is [8,16] in this case. Using recursion would allow you to apply a list of numbers to a list of functions.
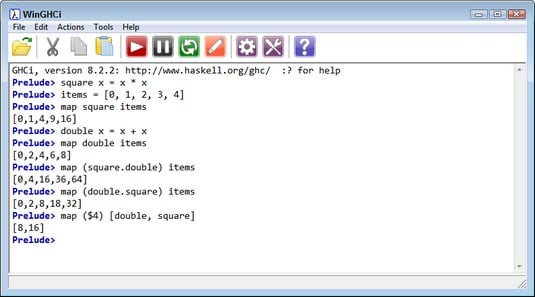 You can apply a single value to a list of functions.
You can apply a single value to a list of functions.Performing data mapping tasks with Python
Python performs many of the same mapping tasks as Haskell, but often in a slightly different manner. Look, for example, at the following code:square = lambda x: x**2 double = lambda x: x + x items = [0, 1, 2, 3, 4]You obtain the same output as you would with Haskell using similar code. However, note that you must convert theprint(list(map(square, items))) print(list(map(double, items)))
map object to a list object before printing it. Given that Python is an impure language, creating code that processes a list of inputs against two or more functions is relatively easy, as shown in this code:
funcs = [square, double]Note that, as with the Haskell code, you're actually applying individual list values against the list of functions. However, Python requires a lambda function to get the job doe. Here’s the output.for i in items: value = list(map(lambda items: items(i), funcs))
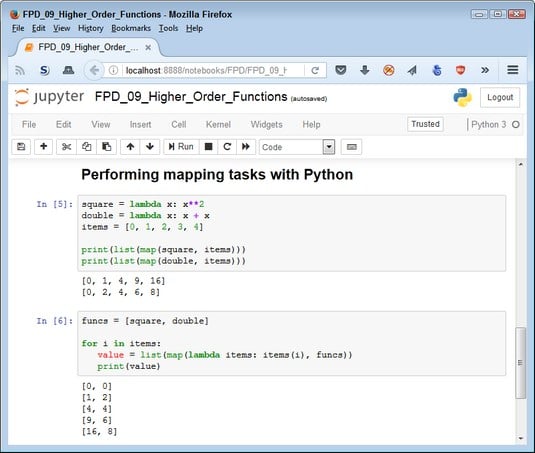 Using multiple paradigms in Python makes mapping tasks easier.
Using multiple paradigms in Python makes mapping tasks easier.

