Knowing the distinct number of objects is useful in various situations, such as when you want to know how many distinct users have seen a certain website page or the number of distinct search engine queries. Storing all the elements and finding the duplicates among them can't work with millions of elements, especially coming from a stream. When you want to know the number of distinct objects in a stream, you still have to rely on a hash function, but the approach involves taking a numeric sketch.
Sketching means taking an approximation, that is an inexact yet not completely wrong value as an answer. Approximation is acceptable because the real value is not too far from it. In this smart algorithm, HyperLogLog, which is based on probability and approximation, you observe the characteristics of numbers generated from the stream. HyperLogLog derives from the studies of computer scientists Nigel Martin and Philippe Flajolet. Flajolet improved their initial algorithm, Flajolet–Martin (or the LogLog algorithm), into the more robust HyperLogLog version, which works like this:
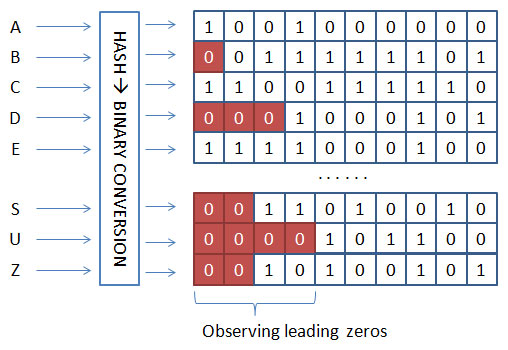
- A hash converts every element received from the stream into a number.
- The algorithm converts the number into binary, the base 2 numeric standard that computers use.
- The algorithm counts the number of initial zeros in the binary number and tracks of the maximum number it sees, which is n.
- The algorithm estimates the number of distinct elements passed in the stream using n. The number of distinct elements is 2^n.
The trick of the algorithm is that if your hash is producing random results, equally distributed (as in a Bloom filter), by looking at the binary representation, you can calculate the probability that a sequence of zeros appeared. Because the probability of a single binary number to be 0 is one in two, for calculating the probability of sequences of zeros, you just multiply that 1/2 probability as many times as the length of the sequence of zeros:
- 50 percent (1/2) probability for numbers starting with 0
- 25 percent (1/2 * 1/2 ) probability for numbers starting with 00
- 12.5 percent (1/2 * 1/2 * 1/2) probability for numbers starting with 000
- (1/2)^k probability for numbers starting with k zeros (you use powers for faster calculations of many multiplications of the same number)
The fewer the numbers that HyperLogLog sees, the greater the imprecision. Accuracy increases when you use the HyperLogLog calculation many times using different hash functions and average together the answers from each calculation, but hashing many times takes time, and streams are fast. As an alternative, you can use the same hash but divide the stream into groups (such as by separating the elements into groups as they arrive based on their arrival order) and for each group, you keep track of the maximum number of trailing zeros. In the end, you compute the distinct element estimate for each group and compute the arithmetic average of all the estimates. This approach is stochastic averaging and provides more precise estimates than applying the algorithm to the entire stream.