For time series data, it's important to know whether the observations continue to have the same mean over time and whether the variance of the data is changing over time.
Many statistical tests and forecasting techniques depend on this assumption.
The figure shows a time series plot of ExxonMobil's daily returns throughout 2013.
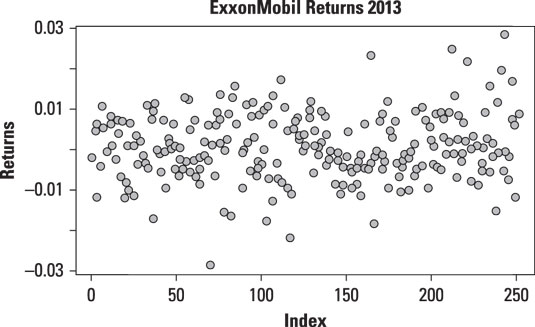
The graph shows that as time elapses, the observations seem to be centered around zero. This indicates that the mean isn't changing over time. If the mean were rising over time, the points on the graph would tend to shift up; if the mean were falling over time, the points on the graph would tend to shift down.
For time series data, it's also important to know whether the variance of the data is changing over time. The figure shows that as time passes, the spread among the observations is growing steadily. (That is, data is becoming more spread out as time elapses.) This indicates that the variance (as well as the standard deviation) is increasing over time.
If the variance is changing over time, that can cause serious problems for many statistical techniques. Fortunately, there are methods available that can correct for this problem.
The situation where variance isn't constant over time has a very intimidating name in econometrics: heteroscedasticity. Pronouncing this word isn't easy!

