A peaking filter for an audio graphic equalizer provides gain or loss (attenuation) at a specific center frequency fc. A peaking filter has unity frequency response magnitude, or 0 dB gain, at frequencies far removed from the center frequency.
At the center frequency fc, the frequency response magnitude in dB is GdB, which is continuously adjustable over a range of, say, +/– 12 dB. These characteristics are encouraging because they fall in line with the design requirements. Before committing to a final design, though, you need additional characterization.
At the same time, the filter complexity is revealed because studying the frequency response means you’ll likely need to work from the system function. From the system function, you can also arrive at the difference equation representation, which is closely related to a filter implementation algorithm.
The heart of the peaking filter is a second-order infinite impulse response (IIR) digital filter:
where the filter parameters are given by
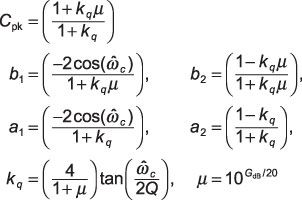
The peaking filter is parameterized in terms of the peak gain, GdB, the center frequency
and a parameter Q, which is inversely proportional to the peaking filter bandwidth. Note that the bandwidth corresponds to a band of frequencies about the center frequency where the filter increases or decreases the signal level relative to unity gain, or 0 dB. The parameter fs is the sampling frequency, typically 44.1 kHz.
Find examples of the peaking filter frequency response in the first figure, which shows the impact of changing just the gain at the center frequency, fc, and in the second figure, which shows the impact of changing Q.
![[Credit: Illustration by Mark Wicker, PhD]](https://www.dummies.com/wp-content/uploads/379733.image3.jpg)
![[Credit: Illustration by Mark Wicker, PhD]](https://www.dummies.com/wp-content/uploads/379734.image4.jpg)
Peaking filters are placed in cascade to form a graphic equalizer. With the peaking filters in cascade, and the gain setting of each filter at 0 dB, the cascade frequency response is unity gain (0 dB) over all frequencies from 0 to fs /2. Figure 3 shows the individual response of six filters set at octave center frequencies according to the formula
fci = 31.25 x 2i Hz, i = 0, 1, . . ., 9
As stated earlier, an octave is a doubling of the frequency. Use Pylab to calculate the center frequencies:
![[Credit: Illustration by Mark Wicker, PhD]](https://www.dummies.com/wp-content/uploads/379735.image5.jpg)
In [336]: 31.25*2**arange(10) Out[336]: array([ 31.25, 62.5 , 125. , 250. , 500. , 1000. , 2000. , 4000. , 8000. , 16000. ])
When the peaking filters are placed in cascade, the responses don’t mesh together perfectly. In fact, the gain flatness in a particular band of frequencies depends on how much gain, GdB, you want to achieve at a particular center frequency, relative to the adjacent frequency bands.
![[Credit: Illustration by Mark Wicker, PhD]](https://www.dummies.com/wp-content/uploads/379736.image6.jpg)

