How to Use Phasors for Circuit Analysis

A phasor is a complex number in polar form that you can apply to circuit analysis. When you plot the amplitude and phase shift of a sinusoid in a complex plane, you form a phase vector, or phasor.

As you might remember from algebra class, a complex number consists of a real part and an imaginary part. For circuit analysis, think of the real part as tying in with resistors that get rid of energy as heat and the imaginary part as relating to stored energy, like the kind found in inductors and capacitors.

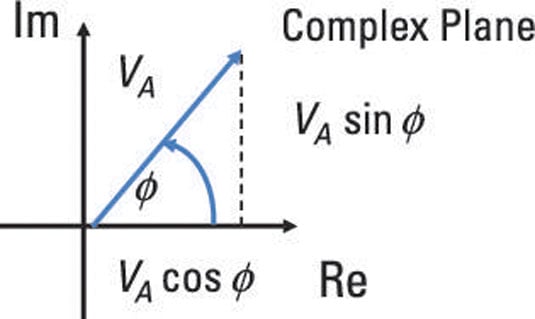
You can also think of a phasor as a rotating vector. Unlike a vector having magnitude and direction, a phasor has magnitude V_A and angular displacement ϕ. You measure angular displacement in the counterclockwise direction from the positive x-axis.

Here is a diagram of a voltage phasor as a rotating vector at some frequency, with its tail at the origin. If you need to add or subtract phasors, you can convert the vector into its x-component (V_A cos ϕ) and its y-component (V_A sin ϕ) with some trigonometry.

The following sections explain how to find the different forms of phasors and introduce you to the properties of phasors.

Find phasor forms

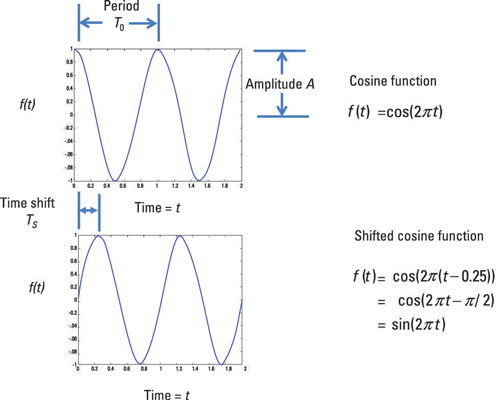
Phasors, which you describe with complex numbers, embody the amplitude and phase of a sinusoidal voltage or current. The phase is the angular shift of the sinusoid, which corresponds to a time shift t₀. So if you have cos[ω(t – t₀)], then ωt₀ = ϕ_O, where ϕ_O is the angular phase shift.

To establish a connection between complex numbers and sine and cosine waves, you need the complex exponential e^jθ and Euler’s formula:

e^jθ = cosθ + jsinθ

where

j = √-1

The left side of Euler’s formula is the polar phasor form, and the right side is the rectangular phasor form. You can write the cosine and sine as follows:

cosθ = Re[e^jθ]

sinθ = Im[e^jθ]

In the equations shown here, Re[ ] denotes the real part of a complex number, and Im[ ] denotes the imaginary part of a complex number.

Here is a cosine function and a shifted cosine function with a phase shift of π/2.

In general, for the sinusoids shown here, you have an amplitude V_A, a radian frequency ω, and a phase shift of ϕ given by the following expression:

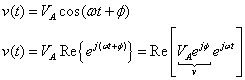
Because the radian frequency ω remains the same in a linear circuit, a phasor just needs the amplitude V_A and the phase ϕ to get into polar form:

V = V_Ae^jϕ

To describe a phasor, you need only the amplitude and phase shift (not the radian frequency). Using Euler’s formula, the rectangular form of the phasor is

V = V_Acosϕ + jV_Asinϕ

Examine the properties of phasors

One key phasor property is the additive property. If you add sinusoids that have the same frequency, then the resulting phasor is simply the vector sum of the phasors — just like adding vectors:

V = V₁ + V₂ + …V_N

For this equation to work, phasors V₁, V₂, …,V_N must have the same frequency. You find this property useful when using Kirchhoff’s laws.

Another vital phasor property is the time derivative. The time derivative of a sine wave is another scaled sine wave with the same frequency. Taking the derivative of phasors is an algebraic multiplication of jω in the phasor domain. First, you relate the phasor of the original sine wave to the phasor of the derivative:

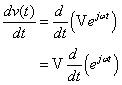
But the derivative of a complex exponential is another exponential multiplied by jω:

Based on the phasor definition, the quantity (jωV) is the phasor of the time derivative of a sine wave phasor V. Rewrite the phasor jωV as

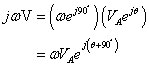
When taking the derivative, you multiply the amplitude V_A by ω and shift the phase angle by 90^o, or equivalently, you multiply the original sine wave by jω. See how the imaginary number j rotates a phasor by 90^o?

Working with capacitors and inductors involves derivatives because things change over time. For capacitors, how quickly a capacitor voltage changes directs the capacitor current. For inductors, how quickly an inductor current changes controls the inductor voltage.