When timing is off in your computer, specific events don’t occur in the right order. But if you know the physics and i-v relationships of resistors and capacitors, you can create a circuit that detects pulses; then when a pulse is missing, the circuit can trigger an alarm notifying the user of a timing problem.
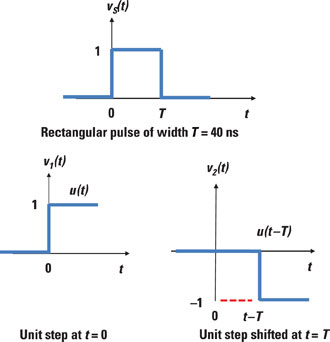
A digital system is controlled by a rectangular clock waveform serving as a standard timing reference. You can model a single rectangular pulse vS(t) as the sum of two step functions, where one of the step functions is delayed and inverted, as you see in the following figure.
Here’s the equation for the rectangular pulse:
VA is the amplitude, which equals 5 volts, u(t) is a step input starting at time t = 0, and u(t – T) is a delayed step function starting at T = 40 nanoseconds.
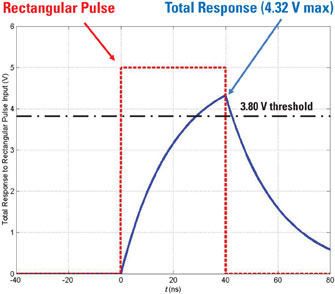
The rectangular waveform serves as an input to the digital device modeled by the following circuit. The output v(t) will detect the clock pulse if v(t) exceeds the logic 1 threshold level of 3.80 volts.
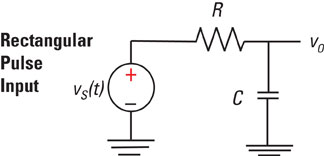
Imagine that you have to find the zero-state response of the voltage v(t) when the time constant RC = 20 ns. Will this circuit detect the rectangular pulse? Here’s how to solve this problem:
Determine the equation for the zero-state response v0.
Zero-state means the initial voltage across the capacitor is zero. As a result, the total response is determined by two inputs given in the rectangular waveform vs(t):
A positive step input with a 5-volt amplitude step function applied at t = 0
A negative step input with a 5-volt amplitude step function applied at t = 40 ns
Here’s the formula for the zero-state response for a step input RC (resistor-capacitor) series circuit:
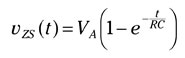
VA is the amplitude of a step input, and RC is the time constant with R as the resistor value and C as the capacitor value.
Determine the response due to the positive step input applied at t = 0.
The zero-state response is given by
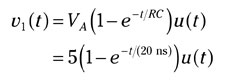
The response v1(t) begins at time zero and reaches a final value of 5 volts after 5 time constants (5RC, or 100 ns). At t = T = 40 ns (two time constants equal to the width of the rectangular pulse), the response v1(t) is
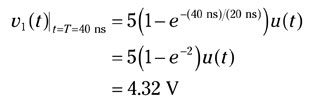
Determine the response due to the negative step input applied at t = 40 ns.
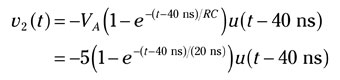
The second response starts at t = T = 40 ns, and the response is equal and opposite to v1(t) but is delayed by 40 nanoseconds. Before t = 40 ns, v2(t) = 0:
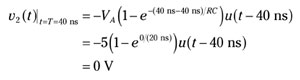
Find the total response vO(t).
You can find the total response by adding v1(t) and v2(t):
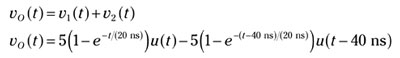
The following figure shows that the total response at t = 40 ns is vO(40 ns) = 4.32 V. For this example, the circuit will detect the clock pulse because the total response reaches a maximum of 4.32 volts, exceeding the threshold of 3.8 volts.
If the pulse width is narrowed down to 1 time constant, or 20 nanoseconds, the total response would reach a maximum of 3.16 volts, which is less than 3.8 volts. In that case, the pulse clock wouldn’t be detected.