You might need to know how to build band-stop filters to reject line noise. In your stereo or entertainment system, you have unique sounds coming from your favorite music or movies. Special audio effects, different voices, and diverse instruments are synthesized to form a wide range of frequencies. You select, reject, or boost the bass, treble, and midrange frequencies by using an equalizer consisting of many different filters.
However, at times, an equalizer may not be able to get rid of unwanted noise.
Suppose the local movie theater just installed a new audio system. Unfortunately, an annoying 60-hertz hum is getting through to the speaker system. Without degrading voice quality, you can implement a band-stop filter (or band-reject filter) to get rid of the 60-hertz signal.
The following transfer function, which relates the output and input signals, gives you the band-stop filter:
T(s) is centered at 60 hertz, with a lower cutoff frequency of 40 hertz and an upper cutoff frequency of 80 hertz, rejecting frequencies between 40 and 80 hertz before they go to the speaker system.
To realize T(s), design a filter using resistors, capacitors, and an operational amplifier to get rid of the 60-hertz signal. Follow these steps:
Break down T(s) into simpler, recognizable transfer functions.
The given transfer function is already written as the sum of two simpler transfer functions, so you can identify the low-pass filter TLPF(s) and the high-pass filter THPF(s) as follows:
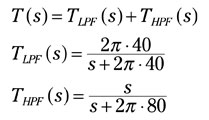
TLPF(s) passes signals below 40 hertz and rejects frequencies above 40 hertz, and THPF(s) passes signals above 80 hertz and rejects frequencies below 80 hertz. The filter outputs are summed, rejecting frequencies between 40 hertz and 80 hertz while passing signals outside this frequency range.
Design the low-pass filter TLPF(s).
Start by rewriting TLPF(s) using impedances of resistors and capacitors described in the Laplace domain:
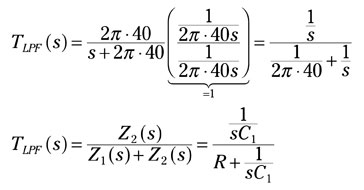
The impedance for a capacitor is Z2(s) = 1/(sC1) = 1/s with C1 = 1 F, and the impedance for a resistor is Z1(s) = R1 = 1/(2p ∙40) W (note that a resistor isn’t frequency dependent — the resistor associates with a constant value).
The equation has the form of a divider equation, which describes the relationship between the desired output variable and input signal as a ratio of the output impedance to the total impedance of a circuit.
These values of capacitance and resistance are impractical in real life, so you need to scale these values so they’re more realistic. Go ahead and scale them by multiplying the numerator and denominator of TLPF(s) by a number k = 106:
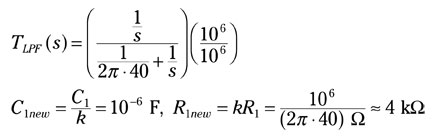
These new values of capacitance and resistance are more realistic. The figure shows the final values of the low-pass design, where now C1 = C1new and R1 = R1new. In general, you have the new scaled values given as C1new = Cold/k and Rnew = kRold.
Design the high-pass filter THPF(s).
Rewriting THPF(s) to show the impedances of resistors and capacitors produces the following equations, where C2 = 1 F (before scaling) and R2 = 1/(2p ∙ 80) Ω (before scaling):
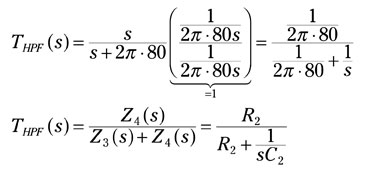
Multiply THPF(s) as follows to scale the resistance and capacitance values:
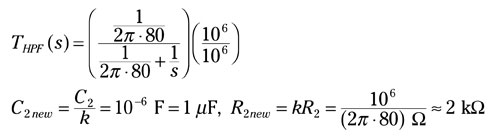
The figure shows the final values of the high-pass design, where now C2 = C2new and R2 = R2new.
Finalize the design of the band-stop filter.
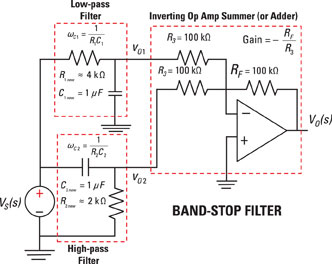
You add up the filter outputs to obtain the band-stop filter by using an inverting summing operational amplifier (op amp). With high-value resistors of 100 kW, you prevent loading effects of the high-pass and low-pass filters. You can see what the final circuit looks like in the following figure.
Note that high values of resistors in an op-amp circuit reduce the accuracy of an ideal op-amp model. However, lower resistor values may involve undesired loading effects. You may need to add op-amp voltage followers to reduce these loading effects. The additional voltage followers increase the complexity and cost of the circuit.