Use superposition to analyze circuits that have lots of voltage and current sources. Superposition helps you to break down complex linear circuits composed of multiple independent sources into simpler circuits that have just one independent source. The total output, then, is the algebraic sum of individual outputs from each independent source.
You can use superposition when faced with a circuit that has three (or more) independent sources. With three independent sources, you find the output voltage of three simplified circuits, where each circuit has one source working and the others turned off. Then add the outputs due to the three power sources.
Circuit A in the sample circuit shown here has two voltage sources and one current source. Suppose you want to find the output voltage across the current source is.
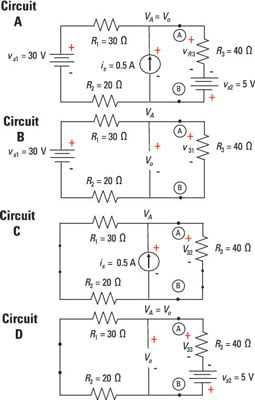
To help you follow the analysis, the voltage vAB is identified by the labels Terminals A and B. This voltage is equal to the output voltage vo across the current source. The voltage across the current source is equivalent to the voltage across resistor R3 connected in series with voltage source vs2.
In Circuit A, the voltage across the current source is is connected in parallel with the series combination of R3 and vs2. You can find the voltage across R3 and vs2, which is equal to the output voltage vo.
Applying Kirchhoff’s voltage law (KVL) to describe this situation, you wind up with
Essentially, finding vo involves finding the voltage across resistor R3. When you know this voltage, you can easily calculate the output voltage, vo, with the preceding equation.
You can break down Circuit A, with three independent sources, into simpler Circuits B, C, and D, each having a single independent source with the other sources removed or turned off. To analyze the simpler circuits with one source, you apply voltage and current divider techniques.
You need to first find the voltage across R3 due to each independent source. Here’s how it works:
Source 1: Circuit B, first voltage source: You calculate the voltage across R3 due to vs1 by first removing the voltage source vs2 and replacing it with a short. You also remove the current source is by replacing it with an open circuit.
After removing two independent sources, you have Circuit B, a series circuit driven by a single voltage source, vs1. Consequently, the voltage divider technique applies, yielding a voltage v31 across resistor R3 due to vs1:
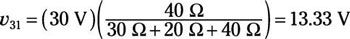
Source 2: Circuit C, current source: You calculate the voltage across R3 due to is by first removing the voltage sources vs1and vs2 and replacing them with shorts.
After removing two independent voltage sources, you have Circuit C, a parallel circuit driven by a single current source is. As a result, the current divider technique applies. This produces a current i32 through resistor R3, resulting from current source is. Also not that the voltage polarity of Vs2 is opposite that of v33. Using the current divider for Circuit C yields the following:
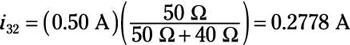
Next, use Ohm’s law to find the voltage across R3 due to current source is:
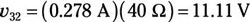
Source 3: Circuit D, second voltage source: You calculate the voltage across R3 due to vs2 by first removing the voltage source vs1 and replacing it with a short circuit. Also remove the current source is by replacing it with an open circuit.
After removing two independent sources, you have Circuit D, a series circuit driven by a single voltage source, vs2. Because this is a series circuit, the voltage divider technique applies, producing a voltage v33 across resistor R3 due to vs2. Also note that the voltage polarity of vs2 is opposite that of v33. Using the voltage divider technique produces the following output:
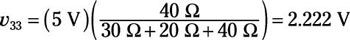
To find vR3, add up the voltages across resistor R3 due to each independent source:
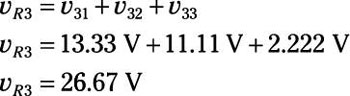
Here’s the total output voltage (vo + vAB) across the current source (or voltage vAB across Terminals A and B):

