In quantum physics, you can break the three-dimensional Schrödinger equation into three one-dimensional Schrödinger equations to make it easier to solve 3D problems. In one dimension, the time-dependent Schrödinger equation (which lets you find a wave function) looks like this:
And you can generalize that into three dimensions like this:
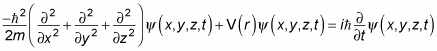
Using the Laplacian operator, you can recast this into a more compact form. Here’s what the Laplacian looks like:
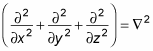
And here’s the 3D Schrödinger equation using the Laplacian:
To solve this equation, when the potential doesn’t vary with time, break out the time-dependent part of the wave function:
Here,
is the solution of the time-independent Schrödinger equation, and E is the energy:
So far, so good. But now you’ve run into a wall — the expression
is in general very hard to deal with, so the current equation is in general very hard to solve.
So what should you do? Well, you can focus on the case in which the equation is separable — that is, where you can separate out the x, y, and z dependence and find the solution in each dimension separately. In other words, in separable cases, the potential, V(x, y, z), is actually the sum of the x, y, and z potentials:
V(x, y, z) = Vx(x) + Vy(y) + Vz(z)
Now you can break the Hamiltonian in
into three Hamilitonians, Hx, Hy, and Hz:
where
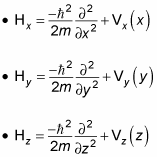
When you divide up the Hamiltonian as in
you can also divide up the wave function that solves that equation. In particular, you can break the wave function into three parts, one for x, y, and z:
Where X(x), Y(y), and Z(z) are functions of the coordinates x, y, and z and are not to be confused with the position operators. This separation of the wave function into three parts is going to make life considerably easier, because now you can break the Hamiltonian up into three separate operators added together:
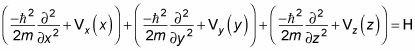
E = Ex + Ey + Ez
So you now have three independent Schrödinger equations for the three dimensions:
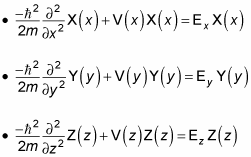
This system of independent differential equations looks a lot easier to solve than
In essence, you’ve broken the three-dimensional Schrödinger equation into three one-dimensional Schrödinger equations. That makes solving 3D problems tractable.

