From a time-independent quantum physics point of view, you can derive the incident wave and scattered wave functions of two spinless nonrelativistic particles. To do so, you need to assume that the interaction between the particles depends only on their relative distance, |r1 – r2|.
You can reduce problems of this kind to two decoupled problems. The first decoupled equation treats the center of mass of the two particles as a free particle, and the second equation is for an effective particle of mass
The first decoupled equation, the free-particle equation of the center of mass, is of no interest to you in scattering discussions. The second equation is the one to concentrate on, where
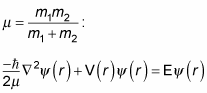
You can use the preceding equation to solve for the probability that a particle is scattered into a solid angle
and you give this probability by the differential cross section,
In quantum physics, wave packets represent particles. In terms of scattering, these wave packets must be wide enough so that the spreading that occurs during the scattering process is negligible (however, the wave packet can't be so spread that it encompasses the whole lab, including the particle detectors). Here's the crux: After the scattering, the wave function breaks up into two parts — an unscattered part and a scattered part. That's how scattering works in the quantum physics world.
Deriving the incident wave function
Assume that the scattering potential V(r) has a very finite range, a. Outside that range, the wave functions involved act like free particles. So the incident particle's wave function, outside the limit of V(r) — that is, outside the range a from the other particle — is given by this equation, because V(r) is zero:
where
The form
is the equation for a plane wave, so
where A is a constant and
is the dot product between the incident wave's wave vector and r. In other words, you're treating the incident particle as a particle of momentum
Deriving the scattered wave function
After the scattering of the spinless particles, the nonscattered wave function isn't of much interest to you, but the scattered wave function is. Although the incident wave function has the form
the scattered wave function has a slightly different form:
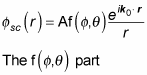
is called the scattering amplitude, and your job is to find it. Here, A is a normalization factor and
where E is the energy of the scattered particle.

