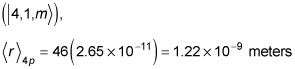When you want to find where an electron is at any given time in a hydrogen atom, what you’re actually doing is finding how far the electron is from the proton. You can find the expectation value of r, that is,
the following expression represents the probability that the electron will be found in the spatial element d3r:
In spherical coordinates,
So you can write
as
The probability that the electron is in a spherical shell of radius r to r + dr is therefore
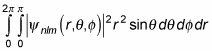
And because
this equation becomes the following:
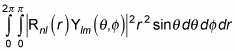
The preceding equation is equal to
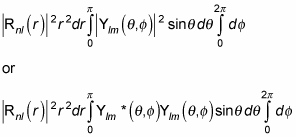
(Remember that the asterisk symbol [*] means the complex conjugate. A complex conjugate flips the sign connecting the real and imaginary parts of a complex number.)
Spherical harmonics are normalized, so this just becomes
Okay, that’s the probability that the electron is inside the spherical shell from r to r + dr. So the expectation value of r, which is
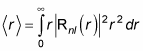
which is
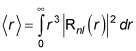
This is where things get more complex, because Rnl(r) involves the Laguerre polynomials. But after a lot of math, here’s what you get:
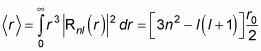
where r0 is the Bohr radius:
The Bohr radius is about
so the expectation value of the electron’s distance from the proton is
So, for example, in the 1s state
the expectation value of r is equal to
And in the 4p state