In quantum physics, you can apply the Schrödinger equation when you work on problems that have a central potential. These are problems where you're able to separate the wave function into a radial part (which depends on the form of the potential) and an angular part, which is a spherical harmonic.
Central potentials are spherically symmetrical potentials, of the kind where V(r) = V(r). In other words, the potential is independent of the vector nature of the radius vector; the potential depends on only the magnitude of vector r (which is r), not on the angle of r.
The Schrödinger equation looks like this in three dimensions, where
is the Laplacian operator:
And the Laplacian operator looks like this in rectangular coordinates:
In spherical coordinates, it's a little messy, but you can simplify later. Check out the spherical Laplacian operator:
Here, L2 is the square of the orbital angular momentum:
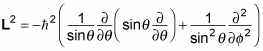
So in spherical coordinates, the Schrödinger equation for a central potential looks like this when you substitute in the terms:
Take a look at the preceding equation. The first term actually corresponds to the radial kinetic energy — that is, the kinetic energy of the particle moving in the radial direction. The second term corresponds to the rotational kinetic energy. And the third term corresponds to the potential energy.
So what can you say about the solutions to this version of the Schrödinger equation? You can note that the first term depends only on r, as does the third, and that the second term depends only on angles. So you can break the wave function,
into two parts:
A radial part
A part that depends on the angles
This is a special property of problems with central potentials.

