Just as with linear motion, you can have acceleration when you’re dealing with angular motion. For example, the line in the figure may be sweeping around the circle faster and faster, which means it’s accelerating.
In linear motion, the following is the equation for acceleration, the rate at which the object’s velocity is changing:
As with all the equations of motion, you need only to substitute the correct angular quantities for the linear ones. In this case, v becomes omega. So the angular acceleration is
The symbol for linear acceleration is a, and the symbol for angular acceleration is alpha, which makes the equation for angular acceleration:
The unit for angular acceleration is radians/s2 (or, technically, just s–2).
Sample question
-
Your toy plane on a string accelerates from omega = 2.1 radians/s to 3.1 radians/s in 1.0 s. What is its angular acceleration?
The correct answer is 1.0 radians/s2.
-
Use the equation for angular acceleration:
-
Plug in the numbers:
-
Practice questions
-
Your model globe is turning at 2.0 radians/s, which you decide isn’t fast enough. So you give it a push, accelerating it in 10–1 s to 5.0 radians/s. What is its angular acceleration?
-
You have a toy plane on a wire, and it’s traveling around in a circle at 3.5 radians/s. You speed it up to 5.4 radians/s in 3.0 s. What was its angular acceleration?
-
You’re square dancing, turning your partner around at 1.0 radians/s. Then you speed up for 0.50 s at an angular acceleration of 10.0 radians/s2. What is your partner’s final angular speed?
-
You’re trying a new yoga move, and starting your arm at rest, you accelerate it at 15 radians/s2 over 1.0 s. What’s your arm’s final angular velocity?
Following are answers to the practice questions:
-
30 radians/s2
-
Use the equation for angular acceleration:
-
Plug in the numbers:
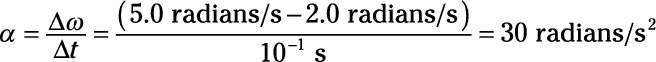
-
-
0.63 radians/s2
-
Use the equation for angular acceleration:
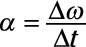
-
Plug in the numbers:
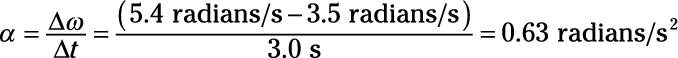
-
-
6.0 radians/s
-
Use the equation for angular acceleration:
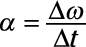
-
Solve:
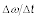
-
Plug in the numbers:
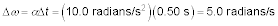
-
Add
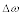
to the original angular velocity:
1.0 radians/s + 5.0 radians/s = 6.0 radians/s
-
-
15 radians/s
-
Use the equation for angular acceleration:
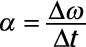
-
Solve:
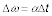
-
Plug in the numbers:
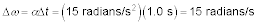
-
Add
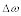
to the original angular velocity:
0 radians/s + 15 radians/s = 15 radians/s
-

