In physics, you can use torque to solve rotational motion problems. For example, you can calculate how much torque is produced by opening a jar of pickles.
Here are some practice questions that you can try.
Practice questions
Torque always points in the direction of what other quantity?
How much torque is produced by opening a jar of pickles if the lid on the jar has a radius of 3.8 centimeters and the force exerted tangentially to the lid is 150 newtons?
Assume that the force is concentrated at one point on the lid. Round your answer to the nearest tenth of a newton-meter.
A 78-gram pendulum swings in a clock, never swinging past an angle of 8 degrees with the vertical.
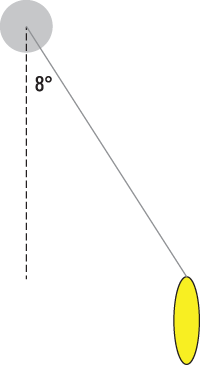
If the pendulum swings on a 2.8-meter-long string attached to a pivot, what is the maximum amount of torque about the pivot? Round your answer to the nearest tenth of a newton-meter.
Answers
The following are the answers to the practice questions:
angular acceleration
Just as force always points in the same direction as linear acceleration, torque points in the same direction as angular acceleration.
5.7 N·m
First, convert the given length into meters:
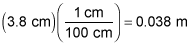
Then use the formula for torque,
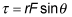
where F is the force exerted, r is the distance from the center of rotation to the point where the force is exerted, and
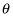
is the angle between the two vectors. The angle here is 90 degrees because the force is exerted tangentially to the lid:
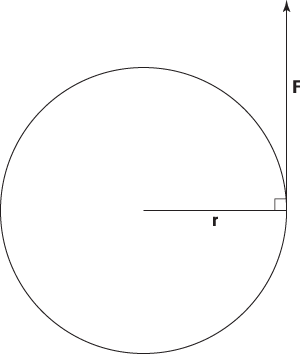
Therefore,

-

First, convert the mass into "correct" units:
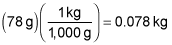
Use the formula for torque,
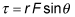
where F is the force exerted, r is the distance from the center of rotation to the point where the force is exerted, and
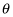
is the angle between the two vectors.
In this problem, the string is the pivot arm, so r = 2.8 meters. The force exerted on it at the point of contact with the pendulum is the force of gravity on the pendulum: the weight of the pendulum. The angle between the two vectors can be seen as either 8 degrees or 172 degrees:
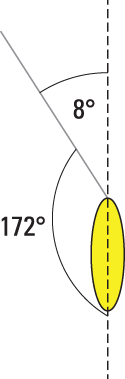
Either number works in the formula, so you can choose to focus on the 8 degree angle. The problem asks you to find the maximum torque — for angles less than 90 degrees, the larger the angle, the larger the sine of the angle will be. So the maximum torque occurs at the maximum angle: 8 degrees. Therefore, the maximum torque is


