String theory's biggest competitor, loop quantum gravity's key insight is that you can describe space as a field; instead of a bunch of points, space is a bunch of lines. The loop in loop quantum gravity has to do with the fact that as you view these field lines (which don’t have to be straight lines, of course), they can loop around and through each other, creating a spin network.
By analyzing this network of space bundles, you can supposedly extract results that are equivalent to the known laws of physics.
The foundation of LQG took place in 1986, when Abhay Ashtekar rewrote general relativity as a series of field lines instead of a grid of points. The result turns out not only to be simpler than the earlier approach, but is similar to a gauge theory.
There’s one problem, though: Gauge theories are background-dependent theories (they are inserted into a fixed space-time framework), but that won’t work, because the field lines themselves represent the geometry of space. You can’t plug the theory into space if space is already part of the theory!
In order to proceed, physicists working in this area had to look at quantum field theory in a whole new way so it could be approached in a background-independent setting. Much of this work was performed by Ashtekar, Lee Smolin, Ted Jacobson, and Carlo Rovelli, who can reasonably be considered among the fathers of loop quantum gravity.
As LQG developed, it became clear that the theory represented a network of connected quantum space bundles, often called “atoms” of space. The failure of previous attempts to write a quantum theory of gravity was that space-time was treated as continuous, instead of being quantized itself.
The evolution of these connections is what provides the dynamic framework of space (although it has yet to be proved that loop quantum gravity actually reduces to the same predictions as those given by relativity).
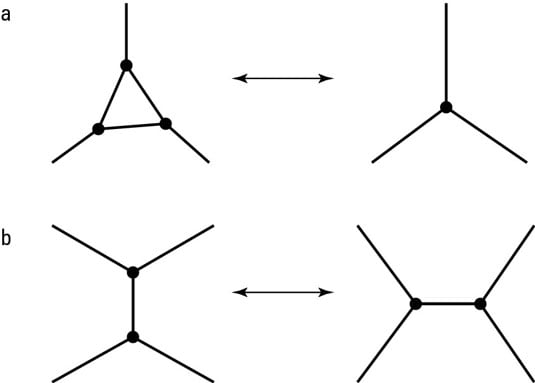
Each atom of space can be depicted with a point (called a node) on a certain type of grid. The grid of all of these nodes, and the connections between them, is called a spin network. (Spin networks were originally developed by Oxford physicist Roger Penrose back in the 1970s.)
The graph around each node can change locally over time, as shown in this figure (which shows the initial state [a] and the new state it changes into [b]). The idea is that the sum total of these changes will end up matching the smooth space-time predictions of relativity on larger scales. (That last bit is the major part that has yet to be proved.)
Now, when you look at these lines and picture them in three dimensions, the lines exist inside of space — but that’s the wrong way to think about it. In LQG, the spin network with all of these nodes and grid lines, the entire spin network, is actually space itself. The specific configuration of the spin network is the geometry of space.
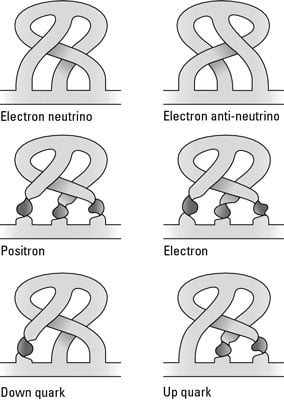
The analysis of this network of quantum units of space may result in more than physicists bargained for, because recent studies have indicated that the Standard Model particles may be implicit in the theory. This work has largely been pioneered by Fotini Markopoulou and work by the Australian Sundance O. Bilson-Thompson.
In Bilson-Thompson’s model, the loops may braid together in ways that could create the particles, as indicated in this figure. (These results remain entirely theoretical, and it remains to be seen how they work into the larger LQG framework as it develops, or whether they have any physical meaning at all.)