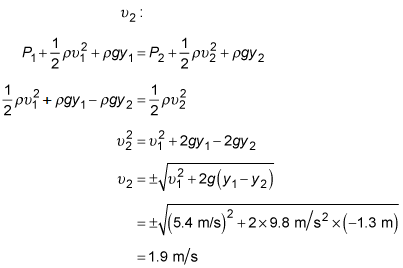Using physics, you can apply Bernoulli's equation to calculate the speed of water. For example, if you know that a dam contains a hole below water level to release a certain amount of water, you can calculate the speed of the water coming out of the hole.
Here are some practice questions that you can try.
Practice questions
A dam holds back the water in a lake. If the dam has a small hole 1.4 meters below the surface of the lake, at what speed does water exit the hole?
A hose lying on the ground has water coming out of it at a speed of 5.4 meters per second. You lift the nozzle of the hose to a height of 1.3 meters above the ground. At what speed does the water now come out of the hose?
Answers
The following are the answers to the practice questions:
5.2 m/s
Use Bernoulli's equation:
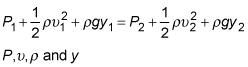
are the pressure, speed, density, and height, respectively, of a fluid. The subscripts 1 and 2 refer to two different points. In this case, let point 1 be on the surface of the lake and point 2 be at the outlet of the hole in the dam. The pressure at each point is just atmospheric pressure, so
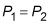
The hole is 1.4 meters below the lake, so
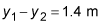
Because the hole is "small," you can assume that the level of the lake doesn't change much as water leaks out of the hole, so
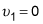
meters per second. Using these equations in Bernoulli's equation, you can solve for the speed of the fluid at point 2:
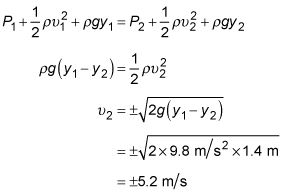
Because you're interested in the speed of the water, which is a positive quantity, use the plus sign in the equation. Thus, the speed of the water coming out of the hole is 5.2 meters per second.
1.9 m/s
Use Bernoulli's equation:
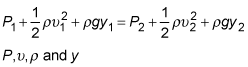
are the pressure, speed, density, and height, respectively, of a fluid. The subscripts 1 and 2 refer to two different points. In this case, let point 1 be on the ground and point 2 be at 1.3 meters above the ground. At both points, the pressure is atmospheric pressure, so
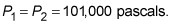
The difference in heights between points 1 and 2 is
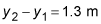
Using these equations, you can solve Bernoulli's equation for the speed