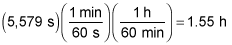In physics, you can use orbital distance to determine how long it takes for an object to revolve around another one. For example, you can calculate how long it takes Mars to travel around the Sun, given its distance from the Sun, in astronomical units.
Here are some practice questions that you can try.
Practice questions
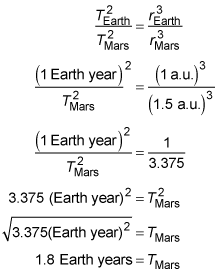
Earth is located 1 a.u. (astronomical unit — a measure of distance) from its sun. In units of "Earth years," how long does Mars take for its own solar revolution if it's located 1.5 a.u. from the sun?
Round your answer to the nearest tenth.
If the International Space Station is located 420 kilometers above Earth's surface, how many hours does it take to make a complete orbit?
Use the following data and round your answer to the nearest hundredth of an hour:
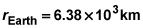
Answers
The following are the answers to the practice questions:
1.8
Kepler's third law states that, given two orbiting bodies A and B, their periods (T) of revolution and distances (r) from the object they're revolving about are related by this equation:
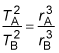
As long as the units match in a ratio, you don't have to convert them to "correct" physics units, so you don't need to convert the astronomical unit values to kilometer values. Given that the period of Earth's revolution is 1 Earth year, the equation is easily solved for Mars's revolution in the same units, which is what you want:
1.55 h
Use the equation relating orbital period to orbital position,
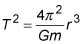
where T is the orbital period, r is the distance between the centers of the orbiter and the orbited, and m is the mass of the orbited body — in this case, Earth, which has a mass of
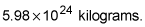
Add the 420 kilometers to Earth's radius to calculate the total distance between the International Space Station's and Earth's centers, and then convert to meters:

Now substitute that into the orbital equation, and you find the International Space Station's orbital period (in units of seconds):

Finally, convert to hours: