For example, take a look at the vector in the image.
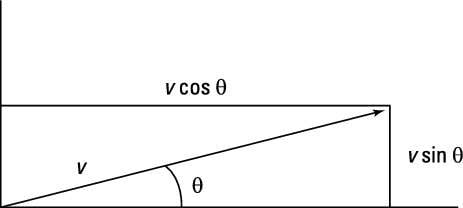
Suppose that you’re given the coordinates of the end of the vector and want to find its magnitude, v, and angle, theta. Because of your knowledge of trigonometry, you know
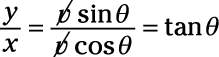
Where tan theta is the tangent of the angle. This means that
theta = tan–1(y/x)Suppose that the coordinates of the vector are (3, 4). You can find the angle theta as the tan–1(4/3) = 53 degrees.
You can use the Pythagorean theorem to find the hypotenuse — the magnitude, v — of the triangle formed by x, y, and v:
Plug in the numbers for this example to get
So if you have a vector given by the coordinates (3, 4), its magnitude is 5, and its angle is 53 degrees.
Sample question
-
Convert the vector given by the coordinates (1.0, 5.0) into magnitude/angle format.
The correct answer is magnitude 5.1, angle 79 degrees.
-
Apply the Pythagorean theorem to find the magnitude. Plug in the numbers to get 5.1.
-
Apply the equation theta= tan–1(y/x) to find the angle. Plug in the numbers to get tan–1(5.0/1.0) = 79 degrees.
-
Practice questions
-
Convert the vector (5.0, 7.0) into magnitude/angle form.
-
Convert the vector (13.0, 13.0) into magnitude/angle form.
-
Convert the vector (–1.0, 1.0) into magnitude/angle form.
-
Convert the vector (–5.0, –7.0) into magnitude/angle form.
-
Magnitude 8.6, angle 54 degrees
-
Apply the equation
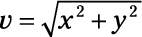
to find the magnitude, which is 8.6.
-
Apply the equation theta = tan–1(y/x) to find the angle: tan–1(7.0/5.0) = 54 degrees.
-
-
Magnitude 18.4, angle 45 degrees
-
Apply the equation
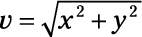
to find the magnitude, which is 18.4.
-
Apply the equation theta = tan–1(y/x) to find the angle: tan–1(13.0/13.0) = 45 degrees.
-
-
Magnitude 1.4, angle 135 degrees
-
Apply the equation
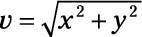
to find the magnitude, which is 1.4.
-
Apply the equation theta = tan–1(y/x) to find the angle: tan–1(1.0/–1.0) = –45 degrees.
However, note that the angle must really be between 90 degrees and 180 degrees because the first vector component is negative and the second is positive. That means you should add 180 degrees to –45 degrees, giving you 135 degrees (the tangent of 135 degrees is also 1.0/–1.0 = –1.0).
-
-
Magnitude 8.6, angle 234 degrees
-
Apply the equation
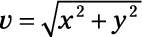
to find the magnitude, which is 8.6.
-
Apply the equation theta = tan–1(y/x) to find the angle: tan–1(–7.0/–5.0) = 54 degrees.
However, note that the angle must really be between 180 degrees and 270 degrees because both vector components are negative. That means you should add 180 degrees to 54 degrees, giving you 234 degrees (the tangent of 234 degrees is also –7.0/–5.0 = 7.0/5.0).
-

