How to Calculate the Latent Heat Needed to Cause a Phase Change

In physics, latent heat is the heat per kilogram that you have to add or remove to make an object change its state; in other words, latent heat is the heat needed to make a phase change happen. Its units are joules per kilogram (J/kg) in the MKS (meter-kilogram-second) system.

Physicists recognize three types of latent heat, corresponding to the changes of phase between solid, liquid, and gas:

• The latent heat of fusion, L_f. This is the heat per kilogram needed to make the change between the solid and liquid phases, as when water turns to ice or ice turns to water.

• The latent heat of vaporization, L_v. This is the heat per kilogram needed to make the change between the liquid and gas phases, as when water boils or when steam condenses into water.

• The latent heat of sublimation, L_s. This is the heat per kilogram needed to make the change between the solid and gas phases, as when dry ice evaporates.

  

Here’s the formula for heat transfer during phase changes, where

m is the mass, and L is the latent heat:

Here, L takes the place of the

and c (specific heat) terms in the temperature-change formula.

Suppose you’re in a restaurant with a glass of 100.0 grams of water at room temperature, 25 degrees Celsius, but you’d prefer ice water at 0 degrees Celsius. How much ice would you need? You can find the answer using the heat formulas for both change in temperature and phase change.

You get out your clipboard, reasoning that the heat absorbed by the melting ice must equal the heat lost by the water you want to cool. Here’s the heat lost by the water you’re cooling:

T is the final temperature, and T₀ is the initial temperature.

Plugging in the numbers tells you how much heat the water needs to lose:

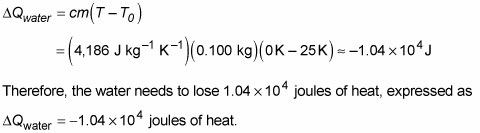
So how much ice would that amount of heat melt? That is, how much ice at 0 degrees Celsius would you need to add to cool the water to 0 degrees Celsius? That would be the following amount, where L_f is the latent heat of fusion for ice:

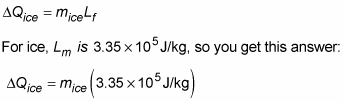
You know this has to be equal to the heat lost by the water, so you can set this equal and opposite to

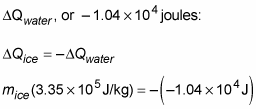
In other words,

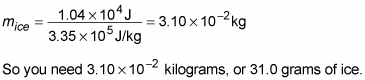
“Pardon me,” you say to the waiter. “Please bring me exactly 31.0 grams of ice at precisely 0 degrees Celsius.”