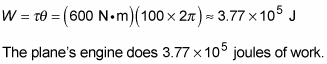In physics, one major player in the linear-force game is work; in equation form, work equals force times distance, or W = Fs. Work has a rotational analog. To relate a linear force acting for a certain distance with the idea of rotational work, you relate force to torque (its angular equivalent) and distance to angle.
When force moves an object through a distance, work is done on the object. Similarly, when a torque rotates an object through an angle, work is done. In this example, you work out how much work is done when you rotate a wheel by pulling a string attached to the wheel’s outside edge (see the figure).
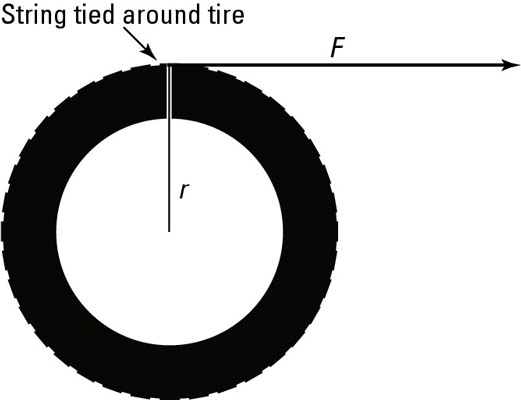
Work is the amount of force applied to an object multiplied by the distance it’s applied. In this case, a force F is applied with the string. Bingo! The string lets you make the handy transition between linear and rotational work. So how much work is done? Use the following equation:
W = Fs
where s is the distance the person pulling the string applies the force over. In this case, the distance s equals the radius multiplied by the angle through which the wheel turns,
so you get

right angles to the radius. So you’re left with
When the string is pulled, applying a constant torque that turns the wheel, the work done equals
This makes sense, because linear work is Fs, and to convert to rotational work, you convert from force to torque and from distance to angle. The units here are the standard units for work — joules in the MKS (meter-kilogram-second) system.
You have to give the angle in radians for the conversion between linear work and rotational work to come out right.
Say that you have a plane that uses propellers, and you want to determine how much work the plane’s engine does on a propeller when applying a constant torque of 600 newton-meters over 100 revolutions. You start with the work equation in terms of torque:
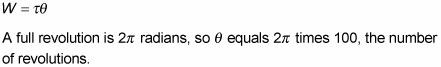
Plugging the numbers into the equation gives you the work: