You can use physics to determine how gravity affects the acceleration of an object as it moves along an inclined plane. When you’re on or near the surface of the Earth, the pull of gravity is constant. It’s a constant force directed straight down with magnitude equal to mg, where m is the mass of the object being pulled by gravity, and g is the magnitude of the acceleration due to gravity:
g = 9.8 meters/second2 = 32.2 feet/second2
Acceleration is a vector, meaning it has a direction and a magnitude, so this equation really boils down to g, an acceleration straight down toward the center of the Earth. The fact that Fgravity = mg is important because it says that the acceleration of a falling body doesn’t depend on its mass:
Fgravity = ma = mg
In other words, ma = mg.
Because a = g, a heavier object doesn’t fall faster than a lighter one. Gravity gives any freely falling body the same acceleration downward (g near the surface of Earth), assuming that no other forces, such as air resistance, are present.
Plenty of gravity-oriented problems in introductory physics involve inclined planes, or ramps. Gravity accelerates objects down ramps — but not the full force of gravity; only the component of gravity acting along the ramp accelerates the object. That’s why an object rolling down a steep ramp rolls quickly: The ramp slopes sharply downward, close to the direction of gravity, so most of the force of gravity can act along the ramp.
To find out how much of the force of gravity accelerates an object on a ramp, you have to break the gravity vector into its components along and perpendicular to the ramp.
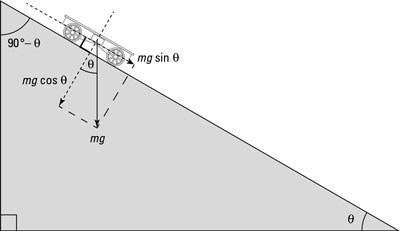
Check out the figure. Here, a cart is about to roll down a ramp. The cart travels not only vertically but also horizontally along the ramp, which is inclined at an angle theta. Say that
and that the length of the ramp is 5.0 meters. How fast will the cart be going at the bottom of the ramp?
You know the length of the ramp, so if you can find the cart’s acceleration along the ramp, you can calculate the cart’s final velocity.

