Study in physics usually begins with linear motion, which is motion in straight lines. Much of physics focuses on angular motion, however, which is the motion of objects around circles or parts of circles. In order to study angular motion you must know how to measure that motion. You use radians, not meters, and you have to know what that means.
Take a look at the figure, where you can see an angle, theta, in a circle. Suppose that theta is 45 degrees. What is that in radians?
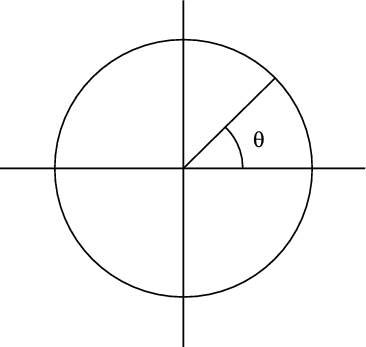
There are 2π radians in a full, 360-degree circle. That means that to convert 45 degrees from degrees to radians, you multiply by 2π/360 degrees, like so:
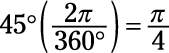
Angles measured in radians don’t have units! That’s because they’re expressed as a fraction of 2π. You’ll sometimes see angles expressed as though radians were units, but technically, they’re not.
The conversion factor, 2π /360 degrees, is usually written as π/180 degrees, which makes this conversion:
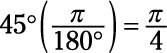
Conversely, to convert from radians to degrees, you multiply by 180 degrees/π. For example, the equation to convert π/4 to an angle looks like this:
Sample question
-
Convert 180 degrees into radians.
The correct answer is π.
-
Use the conversion factor ð/180 degrees.
-
Plug in the numbers:
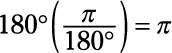
-
Practice questions
-
What is 23 degrees in radians?
-
What is ð/16 in degrees?
Following are answers to the practice questions:
-
0.40 radians
-
Use the conversion factor ð/180 degrees.
-
Plug in the numbers:
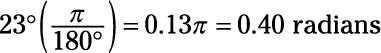
-
-
11.2 degrees
-
Use the conversion factor 180 degrees/ð.
-
Plug in the numbers:
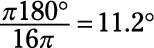
-

