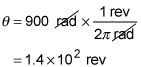Using physics, you can solve problems involving constant angular speed. For example, you can calculate how quickly a child is moving on a merry-go-round given how long it takes for her to travel around from one side to the other.
Here are some practice questions that you can try.
Practice questions
The second hand on a clock is 0.10 meters long. At what speed in meters per second does the tip of the second hand travel?
One parent stands on one side of a merry-go-round and the other parent stands on the opposite side. Their child rides the merry-go-round and takes 15 seconds to travel from one parent to the other parent. What is the child's angular speed in radians per second?
The blades of an electric blender turn at 15 radians per second. How many revolutions do the blades make in 1 minute?
Answers
The following are the answers to the practice questions:
0.010 m/s
Speed is distance traveled divided by the time it takes to travel the distance. The distance traveled by the tip of the second hand is the circumference C of a circle with a radius of r, or
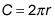
In this problem, the radius is the length of the second hand, so r = 0.10 meters. The time it takes for the tip of the second hand to travel once around the circumference of the circle is T = 60 seconds.
Divide the distance by the time to find the speed:
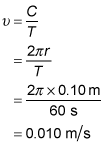
0.21 rad/s
In 15 seconds the child completes one half of a revolution, which is expressed as
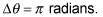
The time it takes is

so the angular speed is
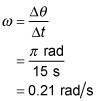

For constant angular motion, the angle
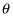
through which an object turns is
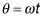
In this case,
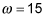
radians per second. Therefore, the angle through which the blades turn in t = 60 seconds is
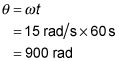
There are

in a revolution, so the conversion factor from radians to revolutions is
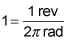
So, the number of revolutions made by the blade is